题目内容
双曲线 的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一 象限内且在l1上,若l2⊥PF1,l2∥PF2,则双曲线的离心率是( )
的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一 象限内且在l1上,若l2⊥PF1,l2∥PF2,则双曲线的离心率是( )A.

B.2
C.

D.

【答案】分析:由双曲线 的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一 象限内且在l1上,知F1(-c,0)F2(c,0)P(x,y),由渐近线l1的直线方程为y=
的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一 象限内且在l1上,知F1(-c,0)F2(c,0)P(x,y),由渐近线l1的直线方程为y= x,渐近线l2的直线方程为y=-
x,渐近线l2的直线方程为y=- x,l2∥PF2,知ay=bc-bx,由ay=bx,知P(
x,l2∥PF2,知ay=bc-bx,由ay=bx,知P( ),由此能求出离心率.
),由此能求出离心率.
解答:解:∵双曲线 的左、右焦点分别为F1,F2,
的左、右焦点分别为F1,F2,
渐近线分别为l1,l2,点P在第一 象限内且在l1上,
∴F1(-c,0)F2(c,0)P(x,y),
渐近线l1的直线方程为y= x,渐近线l2的直线方程为y=-
x,渐近线l2的直线方程为y=- x,
x,
∵l2∥PF2,∴ ,即ay=bc-bx,
,即ay=bc-bx,
∵点P在l1上即ay=bx,
∴bx=bc-bx即x= ,∴P(
,∴P( ),
),
∵l2⊥PF1,
∴ ,即3a2=b2,
,即3a2=b2,
因为a2+b2=c2,
所以4a2=c2,即c=2a,
所以离心率e= =2.
=2.
故选B.
点评:本题考查双曲线的简单性质的应用,解题时要认真审题,仔细解答,注意直线和双曲线位置关系的灵活运用.
 的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一 象限内且在l1上,知F1(-c,0)F2(c,0)P(x,y),由渐近线l1的直线方程为y=
的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一 象限内且在l1上,知F1(-c,0)F2(c,0)P(x,y),由渐近线l1的直线方程为y= x,渐近线l2的直线方程为y=-
x,渐近线l2的直线方程为y=- x,l2∥PF2,知ay=bc-bx,由ay=bx,知P(
x,l2∥PF2,知ay=bc-bx,由ay=bx,知P( ),由此能求出离心率.
),由此能求出离心率.解答:解:∵双曲线
 的左、右焦点分别为F1,F2,
的左、右焦点分别为F1,F2,渐近线分别为l1,l2,点P在第一 象限内且在l1上,
∴F1(-c,0)F2(c,0)P(x,y),
渐近线l1的直线方程为y=
 x,渐近线l2的直线方程为y=-
x,渐近线l2的直线方程为y=- x,
x,∵l2∥PF2,∴
 ,即ay=bc-bx,
,即ay=bc-bx,∵点P在l1上即ay=bx,
∴bx=bc-bx即x=
 ,∴P(
,∴P( ),
),∵l2⊥PF1,
∴
 ,即3a2=b2,
,即3a2=b2,因为a2+b2=c2,
所以4a2=c2,即c=2a,
所以离心率e=
 =2.
=2.故选B.
点评:本题考查双曲线的简单性质的应用,解题时要认真审题,仔细解答,注意直线和双曲线位置关系的灵活运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
 (2011•天津模拟)如图,椭圆
(2011•天津模拟)如图,椭圆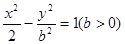 的左、右焦点分别是
的左、右焦点分别是 、
、 ,其一条渐近线方程为
,其一条渐近线方程为 ,点
,点 在双曲线上.则
在双曲线上.则 ·
· =
=