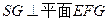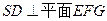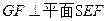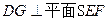题目内容
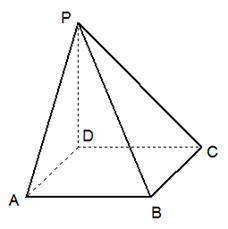
(本题满分14分).如图,在棱长为4的正方体ABCD-A1B1C1D1中,E是D1C1上的一点且EC1=3D1 E,
(1) 求直线BE与平面ABCD所成角的正切值;
(2)求异面直线BE与CD所成角的余弦值.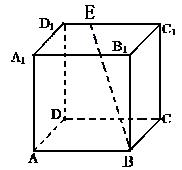
(1) 求直线BE与平面ABCD所成角的正切值;
(2)求异面直线BE与CD所成角的余弦值.

(1) 为直线BE与平面ABCD所成角的正切值为
为直线BE与平面ABCD所成角的正切值为
(2)异而直线BE与CD所成角的余弦值为
 为直线BE与平面ABCD所成角的正切值为
为直线BE与平面ABCD所成角的正切值为
(2)异而直线BE与CD所成角的余弦值为

(1) 在DC上取一点F, 使DF="1," 连结EF,
则EF 平面ABCD, 3分
平面ABCD, 3分
再连结FB,则 为直线BE与平面ABCD所成角,
为直线BE与平面ABCD所成角,
4分
 ,
, 故
故 为直线BE与平面
为直线BE与平面
ABCD所成角的正切值为 ……7分
……7分
(2)由题意AB//CD, (或其补角)是异面直线
(或其补角)是异面直线
 与DC所成的角. …9分
与DC所成的角. …9分
连结AD1与AE,在Rt△AD1E中,可得 ,10分
,10分
又在Rt△BEC1中,可得 , 11分
, 11分
 ……13分
……13分
∴异而直线BE与CD所成角的余弦值为 ……14分
……14分
则EF
 平面ABCD, 3分
平面ABCD, 3分再连结FB,则
 为直线BE与平面ABCD所成角,
为直线BE与平面ABCD所成角, 4分
 ,
, 故
故 为直线BE与平面
为直线BE与平面ABCD所成角的正切值为
 ……7分
……7分(2)由题意AB//CD,
 (或其补角)是异面直线
(或其补角)是异面直线
 与DC所成的角. …9分
与DC所成的角. …9分连结AD1与AE,在Rt△AD1E中,可得
 ,10分
,10分又在Rt△BEC1中,可得
 , 11分
, 11分 ……13分
……13分∴异而直线BE与CD所成角的余弦值为
 ……14分
……14分
练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
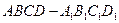 中,以正方体的三条棱所在直线为轴建立空间直角坐标系
中,以正方体的三条棱所在直线为轴建立空间直角坐标系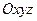 ,
,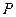 在线段
在线段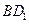 上,且满足
上,且满足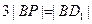 ,试写出点
,试写出点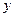 轴的对称点
轴的对称点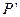 的坐标;
的坐标;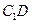 上找一点
上找一点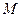 ,使得点
,使得点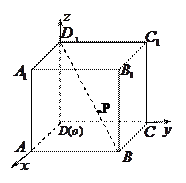
 平面BCD;
平面BCD;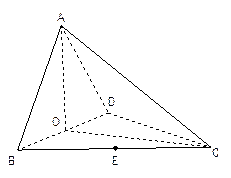

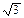 的圆柱,求圆柱的表面积
的圆柱,求圆柱的表面积
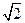 .
.
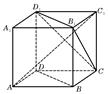
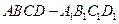 的棱长为
的棱长为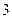 ,点
,点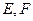 在线段
在线段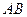 上,点
上,点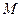 在线段
在线段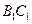 上,点
上,点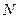 在线段
在线段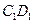 上,且
上,且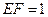 ,
,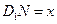 ,
,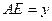 ,
,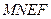 的体积( )
的体积( )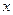 有关,与
有关,与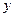 无关
无关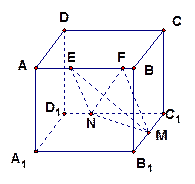
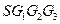 中,E、F分别是边
中,E、F分别是边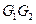 、
、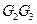 的中点,沿SE、SF及EF把这个正方形折成一个几何体如图(2),使
的中点,沿SE、SF及EF把这个正方形折成一个几何体如图(2),使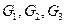 三点重合于G, 下面结论成立的是( )
三点重合于G, 下面结论成立的是( )