题目内容
 已知几何体M的正视图是一个面积为2π的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为( )
已知几何体M的正视图是一个面积为2π的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为( )分析:由三视图可知,该几何体是圆锥的一半,如图所示,据此可求圆锥的底面半径以及圆锥的高,求出答案.
解答: 解:由三视图可知,该几何体是圆锥的一半,如图所示:几何体M的正视图是一个面积为2π的半圆,所以圆锥的底面半圆的底面半径为:
解:由三视图可知,该几何体是圆锥的一半,如图所示:几何体M的正视图是一个面积为2π的半圆,所以圆锥的底面半圆的底面半径为:
πR2=2π,R=2,
因为俯视图是正三角形,所以圆锥的母线长为:4,所以圆锥的高为:2
.
∴S表面积=
×4π×2+2π+
×42=6π+4
.
V体积=
×2π×2
=
π.
故选C.
 解:由三视图可知,该几何体是圆锥的一半,如图所示:几何体M的正视图是一个面积为2π的半圆,所以圆锥的底面半圆的底面半径为:
解:由三视图可知,该几何体是圆锥的一半,如图所示:几何体M的正视图是一个面积为2π的半圆,所以圆锥的底面半圆的底面半径为:| 1 |
| 2 |
因为俯视图是正三角形,所以圆锥的母线长为:4,所以圆锥的高为:2
| 3 |
∴S表面积=
| 1 |
| 2 |
| ||
| 4 |
| 3 |
V体积=
| 1 |
| 3 |
| 3 |
4
| ||
| 3 |
故选C.
点评:由三视图正确恢复原几何体是解决问题的关键,考查空间想象能力以及计算能力.

练习册系列答案
相关题目

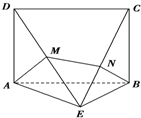 (2012•深圳一模)如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE=
(2012•深圳一模)如图所示的几何体中,四边形ABCD是矩形,平面ABCD⊥平面ABE,已知AB=2,AE=BE= 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为

 和
和
 的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为
的半圆,俯视图是正三角形,那么这个几何体的表面积和体积为

 和
和