Question

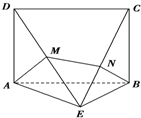（2012•深圳一模）如图所示的几何体中，四边形ABCD是矩形，平面ABCD⊥平面ABE，已知AB=2，AE=BE=

3

，且当规定正视图方向垂直平面ABCD时，该几何体的侧视图的面积为

2

2

．若M、N分别是线段DE、CE上的动点，则AM+MN+NB的最小值为

3

．

Answer 1

分析：由几何体的侧视图的面积为

2

2

求出几何体的高AD，再四棱锥E-ABCD的侧面AED、DEC、CEB展开铺平，在平面内利用余弦定理求得线段AM+MN+NB长为所求．

解答：解：取AB中点F，∵AE=BE=

3

，∴EF⊥AB，
∵平面ABCD⊥平面ABE，∴EF⊥平面ABCD，
易求EF=

2

，
左视图的面积S=

1

2

AD•EF=

1

2

×

2

AD=

2

2

，
∴AD=1，∴∠AED=∠BEC=30°，∠DEC=60°，
将四棱锥E-ABCD的侧面AED、DEC、CEB展开铺平如图，
则AB²=AE²+BE²-2AE•BE•cos120°=3+3-2×3×（-

1

2

）=9，
∴AB=3，
∴AM+MN+BN的最小值为3．
故答案为：3．

点评：本题考查由三视图还原实物图，解题的关键是由三视图还原出实物图的几何特征及其度量，还考查曲面距离最值问题，采用化曲面为平面的办法．须具有空间想象能力、转化、计算能力．