题目内容
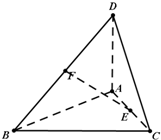如图，三棱锥A-BCD中，AB⊥AD，AC⊥AD，∠BAC=θ（0＜θ≤| π | 2 |
分析：过F作FG⊥AB，垂足为G，连接GE，利用余弦定理求出EG，再根据勾股定理求出EF关于θ的函数式，依据θ的范围求EF的最大值．
解答：解：过F作FG⊥AB，垂足为G，连接GE，
∵AD⊥AB，
∴AD∥FG，∴G为AB的中点，
∴FG=1，AG=1，
∵E为AC的中点，∴AE=1，∠BAC=θ，
∴EG=
∵AD⊥平面ABC，∴FG⊥平面ABC，
在Rt△FGE中，EF=
=
=
，
∵0＜θ≤
，∴EF≤
．
故答案是
．
∵AD⊥AB，
∴AD∥FG，∴G为AB的中点，
∴FG=1，AG=1，
∵E为AC的中点，∴AE=1，∠BAC=θ，
∴EG=
| 12+12-2×1×1×cosθ |
∵AD⊥平面ABC，∴FG⊥平面ABC，
在Rt△FGE中，EF=
| EG2+FG2 |
| 2-2cosθ+1 |
| 3-2cosθ |
∵0＜θ≤
| π |
| 2 |
| 3 |
故答案是
| 3 |
点评：本题考查了棱锥的结构特征及两点间距离的求法，考查了学生的空间想象能力与计算能力．
练习册系列答案
相关题目
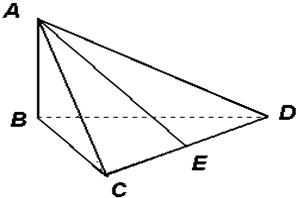如图，三棱锥A-BCD中，AB⊥底面BCD，BC⊥CD，且AB=BC=1，CD=2，点E为CD的中点，则AE的长为（ ）
如图，三棱锥A-BCD，BC=3，BD=4，CD=5，AD⊥BC，E，F分别是棱AB，CD的中点，连接CE，G为CE上一点．
如图，三棱锥A-BCD的底面是等腰直角三角形，AB⊥平面BCD，AB=BC=BD=2，E是棱CD上的任意一点，F、G分别是AC、BC的中点，则在下面的命题中：①平面ABE⊥平面BCD；②平面EFG∥平面ABD；③四面体FECG的体积最大值是
（2009•滨州一模）如图，三棱锥A-BCD中，AD、BC、CD两两互相垂直，且AB=13，BC=3，CD=4，M、N分别为AB、AC的中点．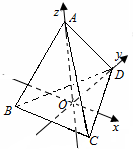
如图，三棱锥A-BCD是正三棱锥，O为底面BCD的中心，以O为坐标原点，分别以OD、OA为y、z轴建立如图所示的空间直角坐标系O-xyz，若