题目内容
已知O为坐标原点,向量 ,点P满足
,点P满足 .
.(Ⅰ)记函数
 •
• ,求函数f(α)的最小正周期;
,求函数f(α)的最小正周期;(Ⅱ)若O,P,C三点共线,求
 的值.
的值.
【答案】分析:(Ⅰ)设 ,由向量的坐标运算求出
,由向量的坐标运算求出 、
、 和
和 的坐标,由
的坐标,由 和向量相等的充要条件求出x和y,求出
和向量相等的充要条件求出x和y,求出 的坐标,由向量的数量积运算
的坐标,由向量的数量积运算 和三角公式化简,再由周期公式求出;
和三角公式化简,再由周期公式求出;
(Ⅱ)根据条件得 ,代入向量共线的坐标条件,由商的关系求出tanα,再由二倍角的正弦公式和平方、商的关系将sin2α用tanα表示出来并求值,再求出
,代入向量共线的坐标条件,由商的关系求出tanα,再由二倍角的正弦公式和平方、商的关系将sin2α用tanα表示出来并求值,再求出 的值.
的值.
解答:解:(Ⅰ)∵
∴ ,
,
设 ,则
,则 ,
,
由 得,
得, ,
,
故 ,则
,则 ,
,
∴f(α)=(sinα-cosα,1)•(2sinα,-1)
=2sin2α-2sinαcosα-1
=-(sin2α+cos2α)
=
∴f(α)的最小正周期T=π.
(Ⅱ)由O,P,C三点共线可得:
则(-1)×(-sinα)=2×(2cosα-sinα),
解得 ,
,
∴ ,
,
∴
= .
.
点评:本题是向量与三角函数的综合题,考查了向量的坐标运算、数量积运算、向量相等的充要条件,三角恒等变换中公式,涉及的公式多,需要熟练掌握并会灵活运用.
 ,由向量的坐标运算求出
,由向量的坐标运算求出 、
、 和
和 的坐标,由
的坐标,由 和向量相等的充要条件求出x和y,求出
和向量相等的充要条件求出x和y,求出 的坐标,由向量的数量积运算
的坐标,由向量的数量积运算 和三角公式化简,再由周期公式求出;
和三角公式化简,再由周期公式求出;(Ⅱ)根据条件得
 ,代入向量共线的坐标条件,由商的关系求出tanα,再由二倍角的正弦公式和平方、商的关系将sin2α用tanα表示出来并求值,再求出
,代入向量共线的坐标条件,由商的关系求出tanα,再由二倍角的正弦公式和平方、商的关系将sin2α用tanα表示出来并求值,再求出 的值.
的值.解答:解:(Ⅰ)∵

∴
 ,
,
设
 ,则
,则 ,
,由
 得,
得, ,
,故
 ,则
,则 ,
,∴f(α)=(sinα-cosα,1)•(2sinα,-1)
=2sin2α-2sinαcosα-1
=-(sin2α+cos2α)
=

∴f(α)的最小正周期T=π.
(Ⅱ)由O,P,C三点共线可得:

则(-1)×(-sinα)=2×(2cosα-sinα),
解得
 ,
,∴
 ,
,∴

=
 .
.点评:本题是向量与三角函数的综合题,考查了向量的坐标运算、数量积运算、向量相等的充要条件,三角恒等变换中公式,涉及的公式多,需要熟练掌握并会灵活运用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
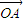 =(sinα,1),
=(sinα,1),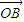 =(cosα,0),
=(cosα,0),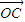 =(-sinα,2),点P是直线AB上的一点,且点B分有向线段
=(-sinα,2),点P是直线AB上的一点,且点B分有向线段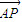 的比为1.
的比为1.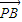 •
•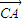 ,α∈(-
,α∈(-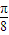 ,
,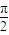 ),讨论函数f(α)的单调性,并求其值域;
),讨论函数f(α)的单调性,并求其值域;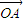 +
+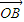 |的值.
|的值.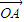 =(sinα,1),
=(sinα,1),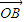 =(cosα,0),
=(cosα,0),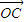 =(-sinα,2),点P是直线AB上的一点,且点B分有向线段
=(-sinα,2),点P是直线AB上的一点,且点B分有向线段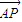 的比为1.
的比为1.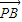 •
•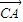 ,α∈(-
,α∈(-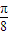 ,
,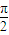 ),讨论函数f(α)的单调性,并求其值域;
),讨论函数f(α)的单调性,并求其值域;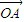 +
+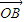 |的值.
|的值.