题目内容

设F₁，F₂分别为双曲线 $数学公式$ 的左、右焦点，点P在双曲线的右支上，且|PF₂|=|₁FF₂|，F₂到直线PF₁的距离等于双曲线的实轴长，则该双曲线的离心率为

A.
$数学公式$
B.
$数学公式$
C.
$数学公式$
D.
$数学公式$

B
分析：利用题设条件和双曲线性质在三角形中寻找等量关系，得出a与b之间的等量关系，即可得到答案．
解答：依题意|PF₂|=|F₁F₂|，可知三角形PF₂F₁是一个等腰三角形，F₂在直线PF₁的投影是其中点，由勾股定理知：
可知|PF₁|=2 $\text{[math]}$ =4b；
根据双曲定义可知4b-2c=2a，整理得c=2b-a，代入c²=a²+b²整理得3b²-4ab=0，求得 $\text{[math]}$ = $\text{[math]}$ ．
∴该双曲线的离心率e= $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ = $\text{[math]}$ ．
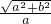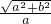故选：B．
点评：本题主要考查三角形与双曲线的相关知识点，突出了对计算能力和综合运用知识能力的考查，属中档题．

练习册系列答案

小学同步学考优化设计小超人作业本系列答案

MOOC淘题一本全练系列答案

小学升创优提分复习一线名师提分作业系列答案

一线名师权威作业本系列答案

初中课堂同步训练系列答案

实验报告册知识出版社系列答案

夺冠百分百新导学初中优化作业本系列答案

初中同步测控优化设计单元测试卷系列答案

全优备考系列答案

世纪金榜全国中考试题精选汇编与分类详解系列答案

相关题目

设F₁、F₂分别为双曲线

=1(a＞0，b＞0)的左、右焦点．若在双曲线右支上存在点P，满足|PF₂|=|F₁F₂|，且F₂到直线PF₁的距离等于双曲线的实轴长，则该双曲线的渐近线方程为（　　）

设F₁、F₂分别为双曲线：

=1（a＞0，b＞0）的左、右焦点，P为双曲线右支上任一点，若

的最小值为8a，则该双曲线的离心率的取值范围是（　　）

A、[3，+∞）

设F₁、F₂分别为双曲线

=1(a＞0，b＞0)的左、右焦点，若在双曲线右支上存在点P，满足PF₂=F₁F₂，且F₂到直线PF₁的距离等于双曲线的实轴长，则该双曲线的渐近线方程为

设F₁，F₂分别为双曲线

=1(a＞0，b＞0)的左、右焦点，以线段F₁F₂为直径的圆交双曲线左支于A，B两点，且∠AF₁B=120°，若双曲线的离心率介于整数k与k+1之间，则k=（　　）

（2011•重庆一模）设F₁、F₂分别为双曲线

=1（a＞0，b＞0）的左、右焦点．若在双曲线右支上存在点P，满足|PF₂|=|F₁F₂|，且点P的横坐标为

c（c为半焦距），则该双曲线的离心率为（　　）