题目内容
边长为2a的正方形ABCD的中心为O,过点O作平面ABCD的垂线,在其上取点V,使OV=h,连接VA,VB,VC,VD,取VC的中点E.
求:(1)cos<
,
>;
(2)若BE⊥VC,求cos<
,
>.
求:(1)cos<
| BE |
| DE |
(2)若BE⊥VC,求cos<
| BE |
| DE |
分析:(1)以O为原点,建立如图所示空间直角坐标系,算出A、B、C、D、V、E各点的坐标,从而得到
=(-
,-
,
),
=(
,
,
),再利用空间向量的夹角公式加以计算,即可得出cos<
,
>的值.
(2)若BE⊥VC,则
•
=
h2-
a2=0,解之得h=
a,再代入(1)中求出的cos<
,
>表达式,即可算出cos<
,
>的值.
| BE |
| 3a |
| 2 |
| a |
| 2 |
| h |
| 2 |
| DE |
| a |
| 2 |
| 3a |
| 2 |
| h |
| 2 |
| BE |
| DE |
(2)若BE⊥VC,则
| BE |
| DE |
| 1 |
| 4 |
| 3 |
| 2 |
| 2 |
| BE |
| DE |
| BE |
| DE |
解答: 解:(1)以O为原点,AB、BC的中点分别在x、y轴上,
解:(1)以O为原点,AB、BC的中点分别在x、y轴上,
建立如图所示空间直角坐标系,可得A(a,-a,0),B(a,a,0),
C(-a,a,0),D(-a,-a,0),V(0,0,h),E(-
,
,
).
∴
=(-
,-
,
),
=(
,
,
),
可得
•
=-
•
+(-
)•
+
•
=
h2-
a2,
=
=
,
=
=
,
∴cos<
,
>=
=
=
;
(2)∵BE⊥VC,
∴
•
=0,可得
h2-
a2=0,解之得h=
a.
由(1)得cos<
,
>=
=
=-
.
 解:(1)以O为原点,AB、BC的中点分别在x、y轴上,
解:(1)以O为原点,AB、BC的中点分别在x、y轴上,建立如图所示空间直角坐标系,可得A(a,-a,0),B(a,a,0),
C(-a,a,0),D(-a,-a,0),V(0,0,h),E(-
| a |
| 2 |
| a |
| 2 |
| h |
| 2 |
∴
| BE |
| 3a |
| 2 |
| a |
| 2 |
| h |
| 2 |
| DE |
| a |
| 2 |
| 3a |
| 2 |
| h |
| 2 |
可得
| BE |
| DE |
| 3a |
| 2 |
| a |
| 2 |
| a |
| 2 |
| 3a |
| 2 |
| h |
| 2 |
| h |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
| |BE| |
(-
|
|
| |DE| |
(
|
|
∴cos<
| BE |
| DE |
| ||||
|
| ||||||||||||
|
| h2-6a2 |
| h2+10a2 |
(2)∵BE⊥VC,
∴
| BE |
| DE |
| 1 |
| 4 |
| 3 |
| 2 |
| 2 |
由(1)得cos<
| BE |
| DE |
| h2-6a2 |
| h2+10a2 |
| 2a2-6a2 |
| 2a2+10a2 |
| 1 |
| 3 |
点评:本题给出特殊的正四棱锥,求
、
所成角的余弦之值,着重考查了利用空间向量研究空间直线所成角的知识,属于中档题.
| BE |
| DE |

练习册系列答案
相关题目
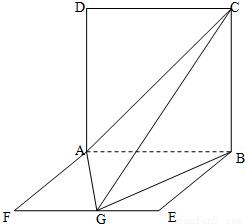
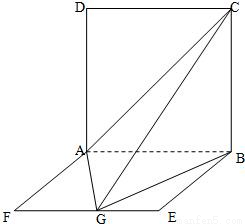
 如图,ABCD是边长为2a的正方形,ABEF是矩形,且二面角C-AB-F是直二面角,AF=a,G是EF的中点.
如图,ABCD是边长为2a的正方形,ABEF是矩形,且二面角C-AB-F是直二面角,AF=a,G是EF的中点.