Question

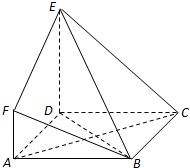
如图，ABCD是边长为2a的正方形，ABEF是矩形，且二面角C-AB-F是直二面角，AF=a，G是EF的中点．
（Ⅰ）求证：平面AGC⊥平面BGC；
（Ⅱ）求GB与平面AGC所成角的大小；
（Ⅲ）求二面角B-AC-G的大小．

Answer 1

分析：法一：（Ⅰ）要证平面AGC⊥平面BGC，只需证明，平面AGC内的直线AG，垂直平面BGC内的两条相交直线BC、BG即可．
（Ⅱ）作BH⊥GC，垂足为H，说明∠BGH是BG与平面AGC所成的角，解三角形BGH，求GB与平面AGC所成角的大小；
（Ⅲ）BH⊥平面AGC．作BO⊥AC，垂足为O，连接HO，说明∠BOH为二面角B-AC-G的平面角，解△CBG求二面角B-AC-G的大小．
法二：以A为原点建立直角坐标系A-xyz，
（Ⅰ）求出向量

AG

，

BG

，

BC

，计算

AG

•

BG

=0，

AG

•

BC

=0证明AG⊥平面BGC，即可．
（Ⅱ）求出平面AGC的一个法向量n，以及

BG

，利用sinθ=

| BG •n|

| BG |•|n|

，求GB与平面AGC所成角的大小；
（Ⅲ）求出平面ABCD的一个法向量，平面AGC的一个法向量n，由|cosα|=

| n • AF |

| AF |•|n|

，求二面角B-AC-G的大小．

解答：解：解法一：（Ⅰ）∵正方形ABCD，
∴CB⊥AB．
又二面角C-AB-F是直二面角，
∴CB⊥平面ABEF．
∵AG?平面ABEF，
∴CB⊥AG．
又AD=2a，AF=a，ABEF是矩形，G是EF的中点，
∴AG=BG=

2

a，AB=2a，AB²=AG²+BG²，
∴BG⊥AG又BC∩BG=B，
∴AG⊥平面CBG，
而AG?平面AGC，故平面AGC⊥平面BGC．（5分）
（Ⅱ）如图，由（Ⅰ）知平面AGC⊥平面BGC，
且交于GC，在平面BGC内作BH⊥GC，垂足为H，则BH⊥平面AGC．
∴∠BGH是BG与平面AGC所成的角．（7分）
∴在Rt△CBG中，BG=

2

a，∴tanBGH=

CB

BG

=

2a

2 a

=

2

．
∴∠BGH=arctan

2

．
即BG与平面AGC所成的角为arctan

2

．（9分）

（Ⅲ）由（Ⅱ），BH⊥平面AGC．作BO⊥AC，垂足为O，连接HO，则HO⊥AC，
∴∠BOH为二面角B-AC-G的平面角．（11分）
∵在Rt△ABC中，BO=

2

a，在Rt△CBG中，BH=

BC•BG

CG

=

2a• 2 a

6 a

=

2 3

3

a．
∴在Rt△BOH中，sinBOH=

BH

BO

=

6

3

，∠BOH=arcsin

6

3

．（13分）
即二面角B-AC-G的大小为arcsin

6

3

．（14分）

解法二：
如图，以A为原点建立直角坐标系A-xyz，
则A（0，0，0），B（0，2a，0），C（0，2a，2a），G（a，a，0），F（a，0，0）．
（Ⅰ）

AG

=（a，a，0），

BG

=
（a，-a，0），

BC

=（0，0，2a），
∴

AG

•

BG

=（a，a，0）•（a，-a，0）=0，

AG

•

BC

=（a，a，0）•（0，0，2a）=0．
∴AG⊥BG，AG⊥BC，
∴AG⊥平面BCG，又AG?平面ACG，
故平面ACG⊥平面BCG．（5分）
（Ⅱ）设GB与平面AGC所成角为θ．
由题意可得

AG

=（a，a，0），

AC

=（0，2a，2a），

BG

=（a，-a，0）．
设平面AGC的一个法向量为n=（x，y，1），
由

AG •n=0 AC •n=0

?

ax+ay=0 2ay+2a=0

?

x=1 y=-1

?n=(1，-1，1)．
∴sinθ=

| BG •n|

| BG |•|n|

=

2a

2 a• 3

=

6

3

．
∴GB与平面AGC所成角的大小为arcsin

6

3

（9分）
（Ⅲ）因n=（1，-1，1）是平面AGC的一个法向量，
又AF⊥平面ABCD，平面ABCD的一个法向量

AF

=（a，0，0），
∴设n与

AF

的夹角为α，得|cosα|=

| n • AF |

| AF |•|n|

=

a

3 a

=

3

3

，
∴二面角B-AC-G的大小为arccos

3

3

．（14分）

点评：本题考查平面与平面垂直，直线与平面所成角及二面角的求法，考查计算能力，空间想象能力，逻辑思维能力，转化思想，是中档题．