题目内容
曲线x2+y2=4与曲线
(θ∈[0，2π))关于直线l对称，则l的方程为（ ）
|
| A、y=x-2 | B、y=x |
| C、y=-x+2 | D、y=x+2 |
分析：先由参数方程可知，表示以（-2，2）为圆心，2为半径的圆．，根据圆的对称性，可判断（0，0）与（-2，2）连线的垂直平分线为直线l，从而得解．
解答：解：由
(θ∈[0，2π))，消去参数得（x+2）2+（y-2）2=4，它表示以（-2，2）为圆心，2为半径的圆．
由题意（0，0）与（-2，2）连线的垂直平分线为直线l，即y=x+2，
故选D．
|
由题意（0，0）与（-2，2）连线的垂直平分线为直线l，即y=x+2，
故选D．
点评：本题主要考查圆的对称性，应注意圆的特殊性，属于基础题．
练习册系列答案
捷径训练检测卷系列答案
小夫子全能检测系列答案
相关题目
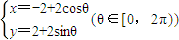关于直线l对称，则l的方程为（ ）
关于直线l对称，则直线l的方程为（ ）。