题目内容
对定义域内的任意两个不相等实数x1,x2下列满足(x1-x2)[f(x1)-f(x2)]<0的函数是
- A.f(x)=x2
- B.f(x)=

- C.f(x)=lnx
- D.f(x)=0.5x
B
分析:判断选项中的函数的单调性,只有在定义域上单调递减的函数方符合题意.
解答:∵A项中f(x)=x2,函数对称轴为x=0,在(-∞,0]上单调减;在[0,+∞)单调增
∴A项不符合题意
∵B项 f(x)= 在定义域内为单调递减函数,假设x1>x2
在定义域内为单调递减函数,假设x1>x2
∴f(x1)<f(x2)
∴有(x1-x2)[f(x1)-f(x2)]<0
同理假设x1<x2,亦可得出结论
∴B项正确.
∵C,D项中的函数均为增函数,假设x1>x2
∴f(x1)<f(x2)
∴有(x1-x2)[f(x1)-f(x2)]>0
同理假设x1<x2,亦可得出此结论.
∴C,D两项均不对
故答案选B
点评:本题主要考查函数单调性的判断与应用.属基础题.
分析:判断选项中的函数的单调性,只有在定义域上单调递减的函数方符合题意.
解答:∵A项中f(x)=x2,函数对称轴为x=0,在(-∞,0]上单调减;在[0,+∞)单调增
∴A项不符合题意
∵B项 f(x)=
 在定义域内为单调递减函数,假设x1>x2
在定义域内为单调递减函数,假设x1>x2∴f(x1)<f(x2)
∴有(x1-x2)[f(x1)-f(x2)]<0
同理假设x1<x2,亦可得出结论
∴B项正确.
∵C,D项中的函数均为增函数,假设x1>x2
∴f(x1)<f(x2)
∴有(x1-x2)[f(x1)-f(x2)]>0
同理假设x1<x2,亦可得出此结论.
∴C,D两项均不对
故答案选B
点评:本题主要考查函数单调性的判断与应用.属基础题.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
对定义域内的任意两个不相等实数x1,x2下列满足(x1-x2)[f(x1)-f(x2)]<0的函数是( )
| A、f(x)=x2 | ||
B、f(x)=
| ||
| C、f(x)=lnx | ||
| D、f(x)=0.5x |
 ,使得对定义域
,使得对定义域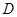 内的任意两个
内的任意两个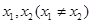 ,均有
,均有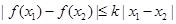 成立,则称函数
成立,则称函数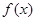 在定义域
在定义域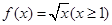 满足利普希茨条件,则常数
满足利普希茨条件,则常数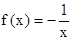 (2)
(2)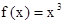 (3)
(3)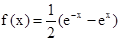
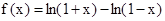 ,其中同时满足:①
,其中同时满足:① ②对定义域内的任意两个自变量
②对定义域内的任意两个自变量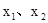 ,都有
,都有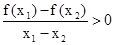 的函数个数为
的函数个数为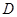 内的任意两个
内的任意两个 ,均有
,均有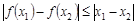 成立,则称函数
成立,则称函数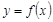 是
是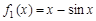 和
和 的单调性并证明;
的单调性并证明;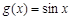 和
和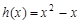 是否为R上的“平缓函数”,并说明理由;
是否为R上的“平缓函数”,并说明理由;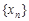 中,
中,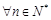 总有
总有 。
。