题目内容
定义:若存在常数 ,使得对定义域
,使得对定义域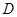 内的任意两个
内的任意两个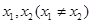 ,均有
,均有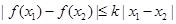 成立,则称函数
成立,则称函数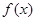 在定义域
在定义域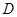 上满足利普希茨条件.若函数
上满足利普希茨条件.若函数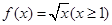 满足利普希茨条件,则常数
满足利普希茨条件,则常数 的最小值为 .
的最小值为 .
【答案】

【解析】
试题分析:由已知中利普希茨条件的定义,若函数 满足利普希茨条件,所以存在常数
满足利普希茨条件,所以存在常数 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个 ,均有
,均有 成立,不妨设
成立,不妨设 ,则
,则 .而
.而 ,所以
,所以 的最小值为
的最小值为 .故选C.
.故选C.
考点:1. 利普希茨条件;2.利用函数的单调性求值域;恒成立问题.

练习册系列答案
相关题目
 的定义域为R,若存在常数
的定义域为R,若存在常数 ,使
,使 对一切实数x均成立,则称
对一切实数x均成立,则称 ②
② ;
; ; ④
; ④ ;
;
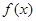 的定义域为
的定义域为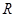 ,若存在常数
,若存在常数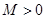 ,使
,使 ≤
≤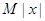 对一切实数
对一切实数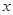 均成立,则称
均成立,则称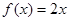 ;
;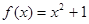 ;
;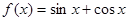 ;
;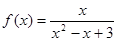 ;
;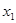 ,
,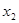 均有
均有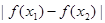 ≤
≤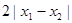 .其中是“倍约束函数”的有 ( )
.其中是“倍约束函数”的有 ( )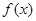 的定义域为
的定义域为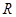 ,若存在常数
,若存在常数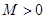 ,使
,使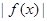 ≤
≤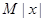 对一切实数
对一切实数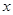 均成立,则称
均成立,则称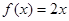 ;
;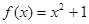 ;
;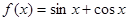 ;
;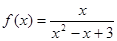 ;
;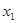 ,
,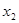 均有
均有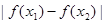 ≤
≤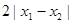 .其中是“倍约束函数”的有 ( )
.其中是“倍约束函数”的有 ( )