题目内容
定义:若对定义域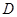 内的任意两个
内的任意两个 ,均有
,均有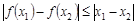 成立,则称函数
成立,则称函数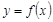 是
是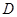 上的“平缓函数”。
上的“平缓函数”。
(1)
判断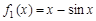 和
和 的单调性并证明;
的单调性并证明;
(2)
判断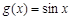 和
和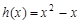 是否为R上的“平缓函数”,并说明理由;
是否为R上的“平缓函数”,并说明理由;
(3)
若数列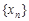 中,
中,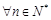 总有
总有 。
。
【答案】
略
【解析】略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案
相关题目
题目内容
定义:若对定义域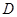 内的任意两个
内的任意两个 ,均有
,均有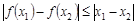 成立,则称函数
成立,则称函数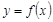 是
是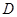 上的“平缓函数”。
上的“平缓函数”。
(1)
判断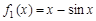 和
和 的单调性并证明;
的单调性并证明;
(2)
判断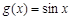 和
和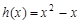 是否为R上的“平缓函数”,并说明理由;
是否为R上的“平缓函数”,并说明理由;
(3)
若数列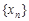 中,
中,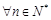 总有
总有 。
。
略
【解析】略

 天天向上一本好卷系列答案
天天向上一本好卷系列答案