题目内容
已知四边形ABCD中,AB∥CD,直线AB、BC、CD、DA交平面α于E、G、F、H,求证:E、F、G、H四点共线.
证明:如下图.
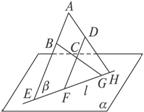
∵AB∥CD,∴AB、CD确定平面β.
∵E、F、G、H分别在直线AB、CD、BC、AD上,
∴E、F、G、H都在β内.
又∵E、F、G、H都在α内,
α、β不是同一个平面且有交点,
∴α、β有且只有一条交线l,即α∩β=l.
∴E、F、G、H∈l,即E、F、G、H共线.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目
题目内容
已知四边形ABCD中,AB∥CD,直线AB、BC、CD、DA交平面α于E、G、F、H,求证:E、F、G、H四点共线.
证明:如下图.

∵AB∥CD,∴AB、CD确定平面β.
∵E、F、G、H分别在直线AB、CD、BC、AD上,
∴E、F、G、H都在β内.
又∵E、F、G、H都在α内,
α、β不是同一个平面且有交点,
∴α、β有且只有一条交线l,即α∩β=l.
∴E、F、G、H∈l,即E、F、G、H共线.

 综合自测系列答案
综合自测系列答案