Question

已知四边形ABCD中，∠BAD=∠ABC=90°，PA⊥平面ABCD，PA=AD=3BC=3，AB=2
（1）求点D到平面PAC的距离；
（2）若点M分

PA

的比为2，求二面角M-CD-A的正切值．

Answer 1

分析：（1）先过D作DQ⊥AC于点Q，由线面垂直的性质定理得PA⊥DQ从而DQ⊥平面PAC，结合三角形中的面积法即可求出D到平面PAC的距离；
（2）过A作AK⊥DC于K点，连MK，由PA⊥平面ABCD，结合线面垂直的性质得出：MK⊥CD，从而有∠MKA为M-CD-A的平面角，利用解三角形即可求出tan∠MKA．

解答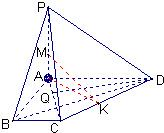：解：（1）过D作DQ⊥AC于点Q，∵PA⊥平面ABCD，
∴PA⊥DQ（1分）
∴DQ⊥平面PAC（2分）
∴又由S△ACD=

1

2

AD•AB=

1

2

AC•DQ，
AC=

AB2+BC2

=

5

（4分）
∴DQ=

AD•AB

AC

=

3•2

5

=

6 5

5

（5分）
∴D到平面PAC的距离为

6 5

5

．（7分）
（2）过A作AK⊥DC于K点，连MK∵PA⊥平面ABCD，∴MK⊥CD
∴∠MKA为M-CD-A的平面角（10分）
∵PA=AD=3，又

PM

MA

=2，∴PM=2，MA=1．在△ACD中，由面积相等，
得AD•AB=CD•AK，又CD=2

2

，
∴AK=

AD•AB

CD

=

3

2

2

，∴tan∠MKA=

MA

AK

=

2

3

．（14分）

点评：本题考查直线与平面垂直，二面角，点的平面的距离，考查空间想象能力，逻辑思维能力，是中档题．