题目内容
已知sinαcosα=
且0＜α＜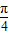
，则cosα-sinα的值是（ ）A．
B．-
C．
D．-
【答案】分析：根据0＜α＜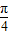
，可得cosα-sinα＞0，利用（cosα-sinα）2=1-2sinαcosα，结合条件，即可求得结论．
解答：解：∵0＜α＜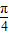
，
∴cosα＞sinα
∴cosα-sinα＞0
∵sinαcosα=
∴（cosα-sinα）2=1-2sinαcosα=1-
=
∴cosα-sinα=
故选A．
点评：本题主要考查了利用同角三角函数关系式，解题的关键是确定cosα-sinα＞0，利用（cosα-sinα）2=1-2sinαcosα，属于基础题
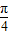，可得cosα-sinα＞0，利用（cosα-sinα）2=1-2sinαcosα，结合条件，即可求得结论．解答：解：∵0＜α＜
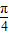，∴cosα＞sinα
∴cosα-sinα＞0
∵sinαcosα=
∴（cosα-sinα）2=1-2sinαcosα=1-
=∴cosα-sinα=
故选A．
点评：本题主要考查了利用同角三角函数关系式，解题的关键是确定cosα-sinα＞0，利用（cosα-sinα）2=1-2sinαcosα，属于基础题
练习册系列答案
相关题目