题目内容
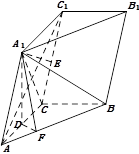
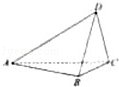
如图,三棱柱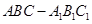 中,点
中,点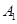 在平面ABC内的射影D在AC上,
在平面ABC内的射影D在AC上,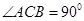 ,
,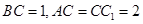 .
.
(1)证明: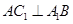 ;
;
(2)设直线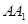 与平面
与平面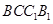 的距离为
的距离为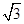 ,求二面角
,求二面角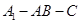 的大小.
的大小.
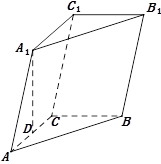
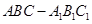 中,点
中,点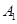 在平面ABC内的射影D在AC上,
在平面ABC内的射影D在AC上,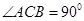 ,
,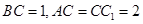 .
.(1)证明:
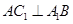 ;
;(2)设直线
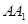 与平面
与平面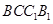 的距离为
的距离为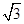 ,求二面角
,求二面角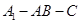 的大小.
的大小.
(1)详见试题分析;(2)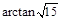 (或
(或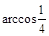 ).
).
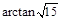 (或
(或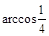 ).
).试题分析:(1)以
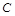 为坐标原点,射线
为坐标原点,射线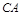 为
为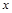 轴的正半轴,以
轴的正半轴,以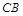 长为单位长,建立空间直角坐标系
长为单位长,建立空间直角坐标系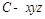 ,计算向量数量积
,计算向量数量积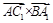 为0,从而证得
为0,从而证得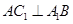 .也可以利用综合法:先由已知
.也可以利用综合法:先由已知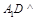 平面
平面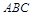 得平面
得平面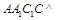 平面
平面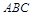 ,再由面面垂直的性质定理证得
,再由面面垂直的性质定理证得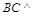 平面
平面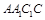 ,而
,而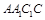 为菱形中
为菱形中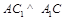 最后由三垂线定理得
最后由三垂线定理得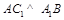 ;(2)向量法:先求平面
;(2)向量法:先求平面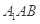 和平面
和平面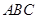 的法向量
的法向量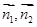 ,再利用公式
,再利用公式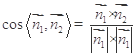 来求二面角
来求二面角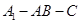 的大小.综合法:先利用三垂线定理或其逆定理作出二面角
的大小.综合法:先利用三垂线定理或其逆定理作出二面角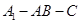 的平面角,再利用解三角形的有关知识求其余弦值大小.
的平面角,再利用解三角形的有关知识求其余弦值大小.试题解析:解法一:(1)
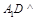 平面
平面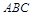 ,
, 平面
平面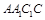 ,故平面
,故平面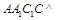 平面
平面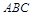 .又
.又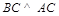 ,
, 平面
平面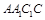 .连结
.连结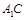 ,∵侧面
,∵侧面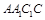 为菱形,故
为菱形,故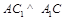 ,由三垂线定理得
,由三垂线定理得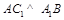 ;(2)
;(2)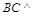 平面
平面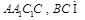 平面
平面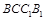 ,故平面
,故平面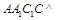 平面
平面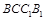 .作
.作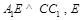 为垂足,则
为垂足,则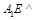 平面
平面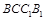 .又直线
.又直线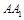 ∥平面
∥平面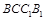 ,因而
,因而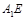 为直线
为直线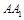 与平面
与平面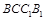 的距离,
的距离,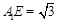 .∵
.∵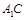 为
为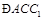 的角平分线,故
的角平分线,故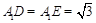 .作
.作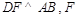 为垂足,连结
为垂足,连结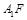 ,由三垂线定理得
,由三垂线定理得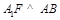 ,故
,故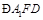 为二面角
为二面角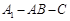 的平面角.由
的平面角.由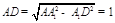 得
得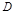 为
为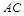 的中点,
的中点,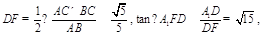 ∴二面角
∴二面角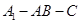 的大小为
的大小为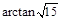 .
.
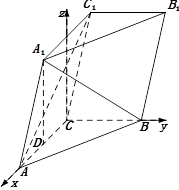
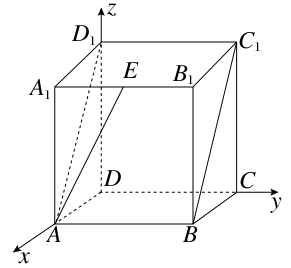
解法二:以
 为坐标原点,射线
为坐标原点,射线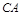 为
为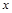 轴的正半轴,以
轴的正半轴,以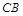 长为单位长,建立如图所示的空间直角坐标系
长为单位长,建立如图所示的空间直角坐标系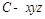 .由题设知
.由题设知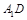 与
与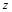 轴平行,
轴平行,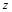 轴在平面
轴在平面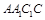 内.
内.(1)设
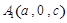 ,由题设有
,由题设有 则
则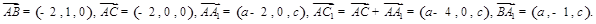 由
由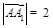 得
得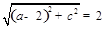 ,即
,即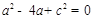 (①).于是
(①).于是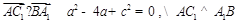 .
.(2)设平面
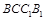 的法向量
的法向量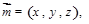 则
则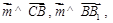 即
即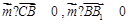 .
.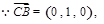
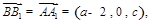 故
故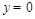 ,且
,且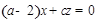 .令
.令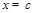 ,则
,则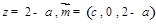 ,点
,点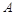 到平面
到平面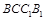 的距离为
的距离为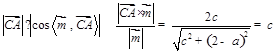 .又依题设,点
.又依题设,点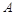 到平面
到平面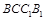 的距离为
的距离为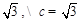 .代入①解得
.代入①解得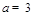 (舍去)或
(舍去)或 .于是
.于是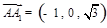 .设平面
.设平面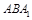 的法向量
的法向量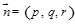 ,则
,则 ,即
,即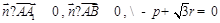 ,故且
,故且 .令
.令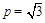 ,则
,则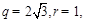
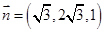 .又
.又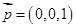 为平面
为平面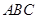 的法向量,故
的法向量,故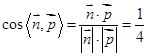 ,∴二面角
,∴二面角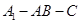 的大小为
的大小为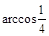 .
.
练习册系列答案
相关题目
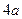 ,将它沿平行于BC的线段PQ折起,使平面APQ⊥平面BPQC,若折叠后AB的长为d,则d的最小值是
,将它沿平行于BC的线段PQ折起,使平面APQ⊥平面BPQC,若折叠后AB的长为d,则d的最小值是
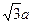
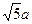
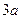
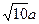
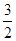 )
)


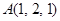 ,
,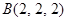 ,点
,点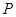 在
在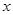 轴上,且
轴上,且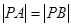 ,则点
,则点 , 则
, 则 两点间距离的最小值是( )
两点间距离的最小值是( )
