题目内容
已知函数f（x）满足f（a+b）=f（a）•f（b），且f（x）＞0（x∈R）若
，则f（-2）等于________．
4
分析：本题考查抽象函数的性质及其应用，可以利用抽象出具体函数求解．f（a+b）=f（a）•f（b）?f（x）=ax（a＞0且a≠1）
解答：（抽象出具体函数）对任意的实数a，b，
都有f（a+b）=f（a）•f（b），且f（1）=
，
则符合条件的一个函数是y=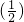
x．
则f（-2）=-2=4．
故答案为：4．
点评：会利用赋值法解决有关抽象函数问题，或者利用抽象函数所给的性质，抽象出一个具体函数求解．
分析：本题考查抽象函数的性质及其应用，可以利用抽象出具体函数求解．f（a+b）=f（a）•f（b）?f（x）=ax（a＞0且a≠1）
解答：（抽象出具体函数）对任意的实数a，b，
都有f（a+b）=f（a）•f（b），且f（1）=
，则符合条件的一个函数是y=
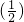x．则f（-2）=
-2=4．故答案为：4．
点评：会利用赋值法解决有关抽象函数问题，或者利用抽象函数所给的性质，抽象出一个具体函数求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目