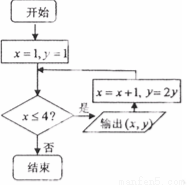
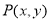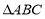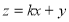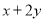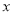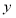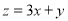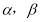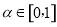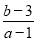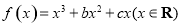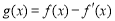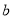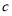题目内容
已知函数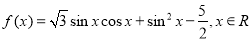 .
.
(1)求函数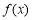 最大值和最小正周期;
最大值和最小正周期;
(2)设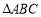 内角
内角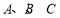 所对的边分别为
所对的边分别为 ,且
,且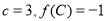 .若
.若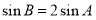 ,求
,求 的值.
的值.
(1)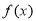 的最大值为
的最大值为 ,最小正周期为
,最小正周期为 ;(2)
;(2)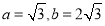 .
.
【解析】
试题分析:(1)先用倍角公式与辅助角公式化简得 ,结合正弦函数的图像与性质可得
,结合正弦函数的图像与性质可得 的最大值,由公式
的最大值,由公式 计算出函数的最小正周期;(2)先由
计算出函数的最小正周期;(2)先由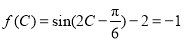 ,结合
,结合 ,确定
,确定 ,用正弦定理化简
,用正弦定理化简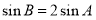 得到
得到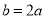 ,再结合余弦定理
,再结合余弦定理 即可解出
即可解出 的值.
的值.
试题解析:(1) 3分
3分
则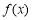 的最大值为
的最大值为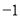 ,最小正周期是
,最小正周期是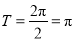 5分
5分
(2) ,则
,则 6分
6分
∵ ,∴
,∴ ,∴
,∴
∴ ,∴
,∴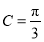 7分
7分
又∵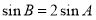 ,由正弦定理得
,由正弦定理得 ,① 9分
,① 9分
由余弦定理得 ,即
,即 ,② 10分
,② 10分
由①②解得 ,
, 12分.
12分.
考点:1.倍角公式;2.三角函数的性质;3.正余弦定理.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目