Question

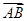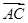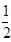设M是△ABC内一点,且·=2,∠BAC=30°,定义f(M)=(m,n,p),其中m、n、p分别是△MBC、△MCA、△MAB的面积,若f(M)=(,x,y),则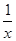+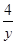的最小值是　　.

 

Answer 1

【答案】

18

【解析】根据题意·=||||cos∠BAC=2,

可得||||=4,

所以S_△ABC=||||sin∠BAC=×4×=1,

则+x+y=1,

即x+y=,

所以+=2(x+y)·(+)=2(1+4++)

≥2×(5+4)=18.

当且仅当=,

即x=,y=时取等号.