题目内容
13.已知复数z=$\frac{2i}{{1+\sqrt{3}\;i}}$(i为虚数单位),$\overline{z}$表示z的共轭复数,则z•$\overline{z}$=1.分析 利用复数代数形式的乘除运算化简z,再由$z•\overline{z}=|z{|}^{2}$求得z•$\overline{z}$.
解答 解:∵z=$\frac{2i}{{1+\sqrt{3}\;i}}$=$\frac{2i(1-\sqrt{3}i)}{(1+\sqrt{3}i)(1-\sqrt{3}i)}=\frac{2\sqrt{3}+2i}{4}=\frac{\sqrt{3}}{2}+\frac{i}{2}$,
∴z•$\overline{z}$=$|z{|}^{2}=(\frac{\sqrt{3}}{2})^{2}+(\frac{1}{2})^{2}=1$.
故答案为:1.
点评 本题考查复数代数形式的乘除运算,是基础的计算题.

练习册系列答案
相关题目
4.已知矩形ABCD中,AB=4$\sqrt{3}$,BC=4,M,N分别是边BC,CD上的点,且MN=2,则$\overrightarrow{AM}•\overrightarrow{AN}$的最小值是( )
| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
1.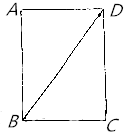 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
 如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )
如图.矩形ABCD中,4BC=3AB,E为矩形ABCD所在平面内一点,若$\overrightarrow{CE}$=λ$\overrightarrow{BD}$且$\overrightarrow{AE}$⊥$\overrightarrow{CE}$,则λ=( )| A. | $\frac{1}{5}$ | B. | $\frac{7}{25}$ | C. | $\frac{8}{25}$ | D. | $\frac{1}{3}$ |

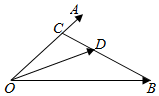 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,C为线段AO上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{4}{9}\overrightarrow{a}$$+\frac{1}{3}\overrightarrow{b}$.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,C为线段AO上距A较近的一个三等分点,D为线段CB上距C较近的一个三等分点,则用$\overrightarrow{a}$,$\overrightarrow{b}$表示$\overrightarrow{OD}$=$\frac{4}{9}\overrightarrow{a}$$+\frac{1}{3}\overrightarrow{b}$.