题目内容
已知各项均为正数的等比数列{an}满足a2a3=a4,a1+a2+a3=21.
(1)求数列{an}的通项公式;
(2)设bn=1+log2an(n∈N)bn=1+log2an(n∈N),求数列{
}的前n项和Sn.
(1)求数列{an}的通项公式;
(2)设bn=1+log2an(n∈N)bn=1+log2an(n∈N),求数列{
| 1 |
| bnbn+1 |
考点:数列的求和
专题:等差数列与等比数列
分析:(1)利用已知条件列出方程求解,首项与公比,即可求数列{an}的通项公式;
(2)化简数列{
}的通项公式,利用裂项法求解数列的前n项和Sn.
(2)化简数列{
| 1 |
| bnbn+1 |
解答:
解:(1)设数列{an}的公比为q,由题意得
(4分)
∵a1>0,q>0,
∴解得a1=1,q=4(6分)
∴{an}的通项公式为an=4n-1(7分)
(2)∵bn=1+log24n-1=1+log222n-2=2n-1(9分)
∴
=
=
(
-
)(11分)
∴Sn=
[(1-
)+(
-
)+…+(
-
)=
(1-
)=
(13分)
|
∵a1>0,q>0,
∴解得a1=1,q=4(6分)
∴{an}的通项公式为an=4n-1(7分)
(2)∵bn=1+log24n-1=1+log222n-2=2n-1(9分)
∴
| 1 |
| bnbn+1 |
| 1 |
| (2n-1)(2n+1) |
| 1 |
| 2 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
∴Sn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 5 |
| 1 |
| 2n-1 |
| 1 |
| 2n+1 |
| 1 |
| 2 |
| 1 |
| 2n+1 |
| n |
| 2n+1 |
点评:本题考查数列求和的基本方法,裂项法的应用,基本知识的考查.

练习册系列答案
相关题目
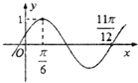 函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<
函数f(x)=Asin(ωx+∅)(A>0,ω>0,|∅|<| π |
| 2 |
| 1 |
| 2 |
A、y=sin(4x+
| ||
B、y=sin(4x+
| ||
C、y=sin(x+
| ||
D、y=sin(x+
|
 如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.
如图,已知四棱锥P-ABCD的底面为直角梯形,AB∥DC,∠DAB=90°,PA⊥底面ABCD,且PA=AD=DC=1,AB=2,M是PB的中点.