题目内容
已知椭圆的两个焦点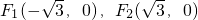 ,且椭圆短轴的两个端点与F2构成正三角形.
,且椭圆短轴的两个端点与F2构成正三角形.
(I)求椭圆的方程;
(Ⅱ)过点(1,0)且与坐标轴不平行的直线l与椭圆交于不同两点P、Q,若在x轴上存在定点E(m,0),使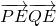 恒为定值,求m的值.
恒为定值,求m的值.
解:(I)由题意可得 c= ,tan30°=
,tan30°= =
= ,∴b=1,∴a=2,
,∴b=1,∴a=2,
故椭圆的方程为 .
.
(Ⅱ) 设直线l的方程为 y-0=k(x-1),即 y=kx-k.
代入椭圆的方程化简可得(1+4k2)x2-8k2x+4k2-4=0,
∴x1+x2=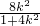 ,x1•x2=
,x1•x2= .
.
∵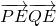 =(m-x1,-y1 )•(m-x2,-y2)=(m-x1)(m-x2)+y1y2
=(m-x1,-y1 )•(m-x2,-y2)=(m-x1)(m-x2)+y1y2
=(m2+k2)+(1+k2)x1•x2-(m+k2)(x1+x2)
=(m2+k2)+(1+k2) -(m+k2)(
-(m+k2)(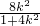 )
)
= 恒为定值,
恒为定值,
∴ ,
,
∴m= .
.
分析:(I) 由题意得到 c= ,tan30°=
,tan30°= =
= ,可得b、a值,即得椭圆的方程.
,可得b、a值,即得椭圆的方程.
(Ⅱ)用点斜式设出直线l的方程,代入椭圆的方程化简,得到根与系数的关系,代入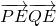 的解析式化简得
的解析式化简得
 恒为定值,故有
恒为定值,故有  ,从而解出m值.
,从而解出m值.
点评:本题考查椭圆的标准方程,以及椭圆的简单性质的应用,一元二次方程根与系数的关系,由
 恒为定值,得到
恒为定值,得到 ,是解题的关键和难点.
,是解题的关键和难点.
 ,tan30°=
,tan30°= =
= ,∴b=1,∴a=2,
,∴b=1,∴a=2,故椭圆的方程为
 .
.(Ⅱ) 设直线l的方程为 y-0=k(x-1),即 y=kx-k.
代入椭圆的方程化简可得(1+4k2)x2-8k2x+4k2-4=0,
∴x1+x2=
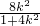 ,x1•x2=
,x1•x2= .
.∵
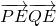 =(m-x1,-y1 )•(m-x2,-y2)=(m-x1)(m-x2)+y1y2
=(m-x1,-y1 )•(m-x2,-y2)=(m-x1)(m-x2)+y1y2 =(m2+k2)+(1+k2)x1•x2-(m+k2)(x1+x2)
=(m2+k2)+(1+k2)
 -(m+k2)(
-(m+k2)(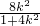 )
) =
 恒为定值,
恒为定值,∴
 ,
,∴m=
 .
.分析:(I) 由题意得到 c=
 ,tan30°=
,tan30°= =
= ,可得b、a值,即得椭圆的方程.
,可得b、a值,即得椭圆的方程.(Ⅱ)用点斜式设出直线l的方程,代入椭圆的方程化简,得到根与系数的关系,代入
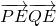 的解析式化简得
的解析式化简得  恒为定值,故有
恒为定值,故有  ,从而解出m值.
,从而解出m值.点评:本题考查椭圆的标准方程,以及椭圆的简单性质的应用,一元二次方程根与系数的关系,由
 恒为定值,得到
恒为定值,得到 ,是解题的关键和难点.
,是解题的关键和难点. 
练习册系列答案
相关题目