题目内容
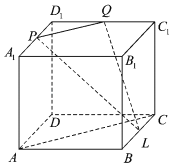
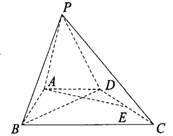
【题目】如图,在三棱锥![]() 中,
中,![]() 是等边三角形,
是等边三角形,![]() ,点
,点![]() 是
是![]() 的中点,连接
的中点,连接![]() .
.

(1)证明:平面![]() 平面
平面![]() ;
;
(2)若![]() ,且二面角
,且二面角![]() 为
为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】
(1)由![]() 是等边三角形,
是等边三角形,![]() ,得
,得![]() .再证明
.再证明![]() ,
,![]() ,从而和证明
,从而和证明![]() 平面
平面![]() ,故平面
,故平面![]() 平面
平面![]() 得证.
得证.
(2)作![]() ,垂足为
,垂足为![]() 连接
连接![]() .由
.由![]() ,证得
,证得![]()
![]() 结合二面角
结合二面角![]() 为
为![]() ,可得
,可得![]() ,
,![]() ,
,![]() .建立空间直角坐标系,求出点的坐标则
.建立空间直角坐标系,求出点的坐标则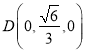 ,
,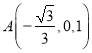 ,向量
,向量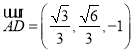 ,即平面
,即平面![]() 的一个法向量
的一个法向量![]() ,运用公式
,运用公式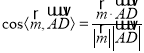 和
和![]() ,即可得出直线
,即可得出直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
解:(1)证明:因为![]() 是等边三角形,
是等边三角形,![]() ,
,
所以![]() ,可得
,可得![]() .
.
因为点![]() 是
是![]() 的中点,则
的中点,则![]() ,
,![]() ,
,
因为![]() ,
,![]() 平面PBD,
平面PBD,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() ,因为
,因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() .
.
(2)如图,作![]() ,垂足为
,垂足为![]() 连接
连接![]() .
.
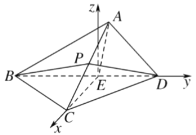
因为![]() ,
,
所以![]()
![]()
![]() 为二面角A-BD-C的平面角.
为二面角A-BD-C的平面角.
由已知二面角![]() 为
为![]() ,知
,知![]() .
.
在等腰三角形![]() 中,由余弦定理可得
中,由余弦定理可得![]() .
.
因为![]() 是等边三角形,则
是等边三角形,则![]() ,所以
,所以![]() .
.
在![]() 中,有
中,有![]() ,得
,得![]() ,
,
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() .
.
则![]() ,
,![]() .
.
以![]() 为坐标原点,以向量
为坐标原点,以向量![]()
![]() 的方向分别为
的方向分别为![]() 轴,
轴,![]() 轴的正方向,
轴的正方向,
以过点![]() 垂直于平面
垂直于平面![]() 的直线为
的直线为![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,
,
则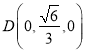 ,
,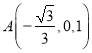 ,向量
,向量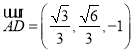 ,
,
平面![]() 的一个法向量为
的一个法向量为![]() ,
,
设直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,
,
则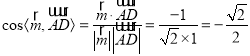 ,
,![]()
所以直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.

 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案【题目】为了解高三学生的“理科综合”成绩是否与性别有关,某校课外学习兴趣小组在本地区高三年级理科班中随机抽取男、女学生各100名,然后对这200名学生在一次联合模拟考试中的“理科综合”成绩进行统计规定:分数不小于240分为“优秀”小于240分为“非优秀”.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有90%以上的把握认为“理科综合”成绩是否优秀与性别有关.
性别 | 优秀 | 非优秀 | 总计 |
男生 | 35 | ||
女生 | 75 | ||
总计 |
(2)用分层抽样的方法从成绩优秀的学生中随机抽取12名学生,然后再从这12名学生中抽取3名参加某高校举办的自主招生考试,设抽到的3名学生中女生的人数为X,求X的分布列及数学期望.
附: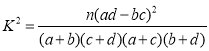 ,其中
,其中![]() .
.
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |