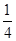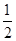题目内容
设函数f(x)=x2+aln(x+1)有两个极值点x1,x2,且x1<x2.
(1)求实数a的取值范围;
(2)当a=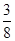 时,判断方程f(x)=-
时,判断方程f(x)=-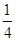 的实数根的个数,并说明理由.
的实数根的个数,并说明理由.
(1)求实数a的取值范围;
(2)当a=
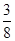 时,判断方程f(x)=-
时,判断方程f(x)=-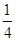 的实数根的个数,并说明理由.
的实数根的个数,并说明理由.(1)0<a< (2)方程f(x)=-
(2)方程f(x)=-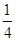 有且只有一个实数根
有且只有一个实数根
 (2)方程f(x)=-
(2)方程f(x)=-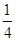 有且只有一个实数根
有且只有一个实数根(1)由f(x)=x2+aln(x+1),可得f′(x)=2x+ (x>-1).
(x>-1).
令g(x)=2x2+2x+a(x>-1),则其对称轴为x=- .由题意可知x1,x2是方程g(x)=0的两个均大于-1的不相等的实数根,其充要条件为
.由题意可知x1,x2是方程g(x)=0的两个均大于-1的不相等的实数根,其充要条件为 解得0<a<
解得0<a<  .
.
(2)由a=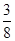 可知x1=-
可知x1=- ,x2=-
,x2=-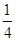 ,从而易知函数y=f(x)在
,从而易知函数y=f(x)在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.
①由y=f(x)在 上单调递增,且f
上单调递增,且f =
= +
+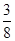 ·ln
·ln =
= -
- ln 2>-
ln 2>-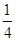 ,以及f
,以及f =
= +
+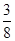 ·ln
·ln =-
=- -
- +
+ <-
<-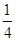 ,故方程f(x)=-
,故方程f(x)=-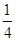 在
在 有且只有一个实根;
有且只有一个实根;
②由于y=f(x)在 上单调递减,在
上单调递减,在 上单调递增,因此f(x)在
上单调递增,因此f(x)在 上的最小值f
上的最小值f =
= +
+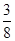 ·ln
·ln =
= +
+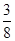 ln
ln >-
>-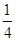 ,故方程f(x)=-
,故方程f(x)=-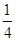 在
在 上没有实数根.
上没有实数根.
综上可知,方程f(x)=-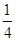 有且只有一个实数根
有且只有一个实数根
 (x>-1).
(x>-1).令g(x)=2x2+2x+a(x>-1),则其对称轴为x=-
 .由题意可知x1,x2是方程g(x)=0的两个均大于-1的不相等的实数根,其充要条件为
.由题意可知x1,x2是方程g(x)=0的两个均大于-1的不相等的实数根,其充要条件为 解得0<a<
解得0<a<  .
.(2)由a=
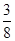 可知x1=-
可知x1=- ,x2=-
,x2=-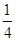 ,从而易知函数y=f(x)在
,从而易知函数y=f(x)在 上单调递增,在
上单调递增,在 上单调递减,在
上单调递减,在 上单调递增.
上单调递增.①由y=f(x)在
 上单调递增,且f
上单调递增,且f =
= +
+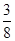 ·ln
·ln =
= -
- ln 2>-
ln 2>-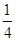 ,以及f
,以及f =
= +
+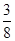 ·ln
·ln =-
=- -
- +
+ <-
<-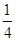 ,故方程f(x)=-
,故方程f(x)=-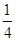 在
在 有且只有一个实根;
有且只有一个实根;②由于y=f(x)在
 上单调递减,在
上单调递减,在 上单调递增,因此f(x)在
上单调递增,因此f(x)在 上的最小值f
上的最小值f =
= +
+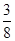 ·ln
·ln =
= +
+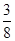 ln
ln >-
>-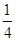 ,故方程f(x)=-
,故方程f(x)=-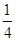 在
在 上没有实数根.
上没有实数根.综上可知,方程f(x)=-
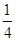 有且只有一个实数根
有且只有一个实数根
练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案 一课一练课时达标系列答案
一课一练课时达标系列答案
相关题目
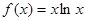 ,
,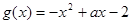 (
(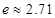 ,
,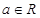 ).
).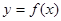 在点(1,
在点(1,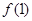 )处的切线与曲线
)处的切线与曲线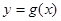 的公共点个数;
的公共点个数;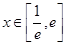 时,若函数
时,若函数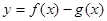 有两个零点,求
有两个零点,求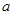 的取值范围.
的取值范围. x+3垂直,求切点坐标与切线的方程.
x+3垂直,求切点坐标与切线的方程.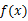 在R上可导,且
在R上可导,且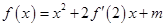 ,则( )
,则( )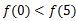
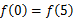
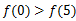
 在区间
在区间 上有极值点,则实数
上有极值点,则实数 的取值范围是( )
的取值范围是( )



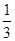 x3+ax2+bx(a,b∈R).
x3+ax2+bx(a,b∈R).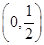 上不存在极值点,求a的取值范围.
上不存在极值点,求a的取值范围.