题目内容
【题目】已知在梯形![]() 中,
中, ![]() 平面
平面![]() ,且
,且![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)连接![]() 交
交![]() 于点
于点![]() ,利用平几知识可得
,利用平几知识可得![]() ,再根据相似比得
,再根据相似比得![]() .最后根据线面平行判定定理得
.最后根据线面平行判定定理得![]() 平面
平面![]() .(2)求二面角大小,一般利用空间向量数量积:先根据条件建立空间直角坐标系,设立各点坐标,列方程组求各平面法向量,利用向量数量积求两法向量夹角,最后根据二面角与法向量夹角关系求二面角.
.(2)求二面角大小,一般利用空间向量数量积:先根据条件建立空间直角坐标系,设立各点坐标,列方程组求各平面法向量,利用向量数量积求两法向量夹角,最后根据二面角与法向量夹角关系求二面角.
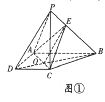
试题解析:解: (Ⅰ)连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() ,如图①所示.
,如图①所示.
∵![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() ,
,
∴![]() .
.
∵![]() 平面
平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
(Ⅱ)设![]() ∵
∵![]() 且
且![]() 平面
平面![]() ,故以
,故以![]() 为原点,过点
为原点,过点![]() 与
与![]() 平行的直线为
平行的直线为![]() 轴,
轴,
![]() 所在直线为
所在直线为![]() 轴,
轴, ![]() 所在直线为
所在直线为![]() 轴,建立空间直角坐标系如图②所示,则
轴,建立空间直角坐标系如图②所示,则

![]() .
.
由![]() ,得
,得![]() ,得
,得![]() .
.
解得![]() ,即
,即![]() ,
,
![]() .
.
设![]() 是平面
是平面![]() 的一个法向量,则
的一个法向量,则![]()
令![]() ,则
,则![]() ,即
,即![]() .
.
取![]() 的中点,记为
的中点,记为![]() ,连接
,连接![]() ,
,
易求得![]() 的坐标为
的坐标为![]() ,
,
∴![]()
![]() .
.
由![]() ,得
,得![]() ,
,
由![]() 底面
底面![]() ,得
,得![]() ,
,
又![]() ,∴
,∴![]() 平面
平面![]() .
.
∴![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
∴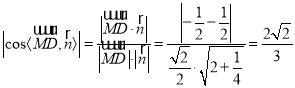 .
.
由图可知二面角![]() 为锐二面角,
为锐二面角,
∴二面角![]() 的余弦值为
的余弦值为![]() .
.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
【题目】PM2.5是指空气中直径小于或等于2.5微米的颗粒物(也称可入肺颗粒物).为了探究车流量与PM2.5的浓度是否相关,现采集到某城市周一至周五某一时间段车流量与PM2.5的数据如表:
时间 | 周一 | 周二 | 周三 | 周四 | 周五 |
车流量x(万辆) | 50 | 51 | 54 | 57 | 58 |
PM2.5的浓度y(微克/立方米) | 69 | 70 | 74 | 78 | 79 |
(1)根据上表数据,请在如图坐标系中画出散点图; 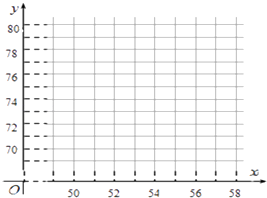
(2)根据上表数据,用最小二乘法求出y关于x的线性回归方程 ![]() ;(保留2位小数)
;(保留2位小数)
(3)若周六同一时间段车流量是25万辆,试根据(2)求出的线性回归方程预测,此时PM2.5的浓度为多少(保留整数)?
参考公式: ![]() =
= 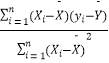 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() .
.