题目内容

定义min{a， b}=
a(a≤b)
b(a＞b)
．已知f（x）=132-x，g（x）=
x
，在f（x）和g（x）的公共定义域内，设m（x）=min{f（x），g（x）}，则m（x）的最大值为______．
因为f（x）=132-x的定义域为R，g（x）=
x
的定义域为[0，+∞），
由132-x≤
x
，解得x≥121．
又min{a， b}=
a(a≤b)
b(a＞b)
，所以
m（x）=min{f（x），g（x）}=
132-x(x≥121)
x
(0≤x＜121)
，
当0≤x＜121时，函数y=
x
为增函数，当x≥121时函数y=132-x为减函数，所以
当132-x=
x
，即x=121时，m（x）最大，最大值为11．
故答案为11．
练习册系列答案
相关题目
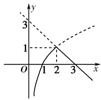精英家教网对于任意实数a，b，定义min{a，b}=
a，a≤b
b，a＞b.
设函数f（x）=-x+3，g（x）=log2x，则函数h（x）=min{f（x），g（x）}的最大值是
 
．
已知函数f(x)=
x
ax+b
(a≠0)满足f（2）=1，且方程f（x）=x有且仅有一个实数根．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）设数列{an}满足a1=1，an+1=f（an）≠1，n∈N*．求数列{an}的通项公式；
（Ⅲ）定义min{a，b}=
a，a≤b
b，a＞b
．对于（Ⅱ）中的数列{an}，令bn=min{an，
1
n
}．设Sn为数列{bn}的前n项和，求证：Sn＞ln（n+1）．
定义min{a， b}=
a(a≤b)
b(a＞b)
．已知f（x）=132-x，g（x）=
x
，在f（x）和g（x）的公共定义域内，设m（x）=min{f（x），g（x）}，则m（x）的最大值为
11
11
．
定义min{a，b，c}为a，b，c中的最小值，设f（x）=min{2x+4，x2+1，5-3x}，则f（x）的最大值是（　　）
（2012•蓝山县模拟）定义min{a，b}=
b，a≥b
a，a＜b.
设实数x，y满足约束条件
x2≤1
y2≤1
，则z=min{2x+y，x-y}的取值范围为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网