题目内容
18.若P是双曲线x2-y2=λ(λ>0)左支上的一点,F1、F2是左、右两个焦点,若|PF2|=6,PF1与双曲线的实轴垂直,则λ的值是( )| A. | 3 | B. | 4 | C. | 1.5 | D. | 1 |
分析 双曲线x2-y2=λ,即$\frac{{x}^{2}}{λ}-\frac{{y}^{2}}{λ}=1$,a=b=$\sqrt{λ}$,c=$\sqrt{2λ}$,利用|PF2|=6,PF1与双曲线的实轴垂直,建立方程,即可求出λ的值.
解答 解:$\frac{{x}^{2}}{λ}-\frac{{y}^{2}}{λ}=1$,则a=$\sqrt{λ}$,b=$\sqrt{λ}$,c=$\sqrt{2λ}$,
由PF1与双曲线的实轴垂直,则P的横坐标为-c,代入双曲线方程,则y=$\sqrt{λ}$,
即丨PF1丨=$\sqrt{λ}$,
36=(6-2$\sqrt{λ}$)2+(2$\sqrt{2λ}$)2,∴λ=4,
故选B.
点评 本题考查双曲线的方程与性质,考查勾股定理的运用,属于中档题.

练习册系列答案
相关题目
14.以(-1,1)为圆心且与直线x-y=0相切的圆的方程是( )
| A. | (x+1)2+(y-1)2=2 | B. | (x+1)2+(y-1)2=4 | C. | (x-1)2+(y+1)2=1 | D. | (x-1)2+(y+1)2=4 |
13.若f(x)=loga(8-ax)(a>0且a≠1)在[0,2]上为减函数,则实数a的范围是( )
| A. | (1,+∞) | B. | (1,4) | C. | (1,4] | D. | (0,1) |
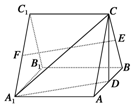 如图,直三棱柱ABC-A1B1C1中,D,E,F分别为棱AB,BC,A1C1的中点.证明:
如图,直三棱柱ABC-A1B1C1中,D,E,F分别为棱AB,BC,A1C1的中点.证明: