题目内容
设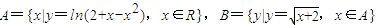 ,则CAB=( )
,则CAB=( )A.(-∞,-1]∪[2,+∞)
B.(-1,0)
C.(-∞,0]∪[2,+∞)
D.(-1,1]
【答案】分析:由题意及已知的两个集合,对于集合A实质为y=ln(2+x-x2)的定义域求出A,对于集合B为 函数的函数的值域,求出B,利用集合的补集定义即可求解.
函数的函数的值域,求出B,利用集合的补集定义即可求解.
解答:解:由于已知A={x|y=ln(2+x-x2)}={x|2+x-x2>0}={x|-1<x<2};
集合B= ,
,
由于-1<x<2,∴1<x+2<4,∴ ,即y∈(1,2),
,即y∈(1,2),
所以B={y|1<y<2},∴CAB=(-1,1],
故选D.
点评:此题考查了集合表示中的描述法,还考查了一元二次不等式的求解及利用解析式选择直接法求函数的值域,属于基本题型.
 函数的函数的值域,求出B,利用集合的补集定义即可求解.
函数的函数的值域,求出B,利用集合的补集定义即可求解.解答:解:由于已知A={x|y=ln(2+x-x2)}={x|2+x-x2>0}={x|-1<x<2};
集合B=
 ,
,由于-1<x<2,∴1<x+2<4,∴
 ,即y∈(1,2),
,即y∈(1,2),所以B={y|1<y<2},∴CAB=(-1,1],
故选D.
点评:此题考查了集合表示中的描述法,还考查了一元二次不等式的求解及利用解析式选择直接法求函数的值域,属于基本题型.

练习册系列答案
相关题目
设A={x|y=ln(2+x-x2),x∈R},B={y|y=
,x∈A},则CAB=( )
| x+2 |
| A、(-∞,-1]∪[2,+∞) |
| B、(-1,0) |
| C、(-∞,0]∪[2,+∞) |
| D、(-1,1] |
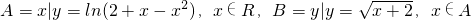 ,则CAB=
,则CAB=