题目内容
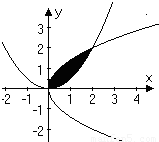
已知曲线C1:y2=2x与C2:y=![]() 在第一象限内交点为P.
在第一象限内交点为P.
(1)求过点P且与曲线C2相切的直线方程;
(2)求两条曲线所围图形(如图所示阴影部分)的面积S.
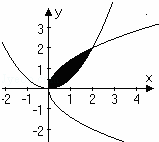
考点:
定积分在求面积中的应用.
专题:
计算题;导数的概念及应用.
分析:
(1)先通过解方程组求交点P的坐标,再根据导数的几何意义求出函数在x=2处的导数,从而得到切线的斜率,再利用点斜式方程写出切线方程即可.
(2)先确定积分区间,再确定被积函数,从而可求由两条曲线曲线C1:y2=2x与C2:y=![]() 所围图形的面积.
所围图形的面积.
解答:
解:(1)曲线C1:y2=2x与C2:y=![]() 在第一象限内交点为P(2,2)
在第一象限内交点为P(2,2)
C2:y=![]() 的导数y'=xy'|x=2=2
的导数y'=xy'|x=2=2
而切点的坐标为(2,2)
∴曲线C2:y=![]() 在x=2的处的切线方程为y﹣2=2(x﹣2),即2x﹣y﹣2=0.(2)由曲线C1:y2=2x与C2:y=
在x=2的处的切线方程为y﹣2=2(x﹣2),即2x﹣y﹣2=0.(2)由曲线C1:y2=2x与C2:y=![]() 可得两曲线的交点坐标为(0,0),(2,2)
可得两曲线的交点坐标为(0,0),(2,2)
∴两条曲线所围图形(如图所示阴影部分)的面积:
S=![]() (
(![]() ﹣
﹣![]() )dx=(
)dx=(![]() ×
×![]() x
x![]() ﹣
﹣![]() )
)![]() =
=![]() .
.
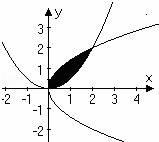
点评:
本题主要考查了利用导数研究曲线上某点切线方程,定积分在求面积中的应用,考查运算求解能力,属于基础题.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
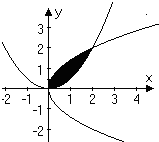 已知曲线C1:y2=2x与C2:y=
已知曲线C1:y2=2x与C2:y=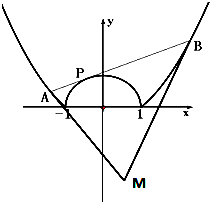 如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.
如图,已知曲线C1:x2+y2=1(|x|<1),C2:x2=8y+1(|x|≥1),动直线l与C1相切,与C2相交于A,B两点,曲线C2在A,B处的切线相交于点M.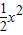 在第一象限内交点为P.
在第一象限内交点为P.