题目内容
7.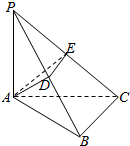 如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,
如图,△ABC是直角三角形,∠ABC=90°,AP⊥平面ABC,且AP=AB,点D是PB的中点,点E是PC上的一点,(1)当DE∥BC时,求证:直线PB⊥平面ADE;
(2)当DE⊥PC时,求证:直线PC⊥平面ADE;
(3)当AB=BC时,求二面角A-PC-B的大小.
分析 (1)证明AP⊥BC,AB⊥BC,推出BC⊥平面PAB,得到BC⊥PB,DE⊥PB,即可证明PB⊥平面ADE.
(2)证明BC⊥AD,AD⊥PC,结合DE⊥PC,即可证明PC⊥平面ADE.
(3)说明∠AED是二面角A-PC-B的平面角,设AP=a,则AB=BC=a,在Rt△ADE中,可求得∠AED=60°,得到二面角A-PC-B的大小.
解答 (1)证:∵AP=AB,点D是PB的中点,∴AD⊥PB,
∵AP⊥平面ABC,BC?平面ABC,
∴AP⊥BC,∵AB⊥BC,∴BC⊥平面PAB,
∵PB?平面PAB,∴BC⊥PB,
∵DE∥BC,∴DE⊥PB,∴PB⊥平面ADE. (4′)
(2)证:∵BC⊥平面PAB,AD?平面PAB,∴BC⊥AD,
又AD⊥PB,∴AD⊥平面PBC,∵PC?平面PBC,
∴AD⊥PC,
又DE⊥PC,∴PC⊥平面ADE. (7′)
(3)解:由(2)可知,当DE⊥PC时,PC⊥平面ADE,
∴∠AED是二面角A-PC-B的平面角. (8′)
设AP=a,则AB=BC=a,$AC=\sqrt{2}a$,$PC=\sqrt{3}a$,(9′)
∵AD⊥平面PBC,DE?平面PBC,∴AD⊥DE,
在Rt△ADE中,可求得,$AD=\frac{{\sqrt{2}}}{2}a$,$AE=\frac{AP•AC}{PC}=\frac{{a•\sqrt{2}a}}{{\sqrt{3}a}}=\frac{{\sqrt{2}}}{{\sqrt{3}}}a$,(10′)
∴$sinAED=\frac{AD}{AE}=\frac{{\sqrt{3}}}{2}$,∴∠AED=60°,
∴二面角A-PC-B的大小为600. (12′)
点评 本题考查直线与平面垂直的判定定理的应用,二面角的平面角的求法,考查空间想象能力以及计算能力.

| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{5}$=1 | B. | $\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{25}$=1 | C. | $\frac{{x}^{2}}{5}$+$\frac{{y}^{2}}{4}$=1 | D. | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1 |
| A. | [-3,1] | B. | (-3,1) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-3)∪(1,+∞) |
| A. | (-∞,-3)∪(-3,0] | B. | (-∞,-3)∪(-3,1] | C. | (-3,0] | D. | (-3,1] |
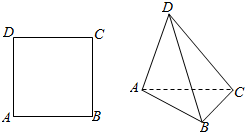 把边长为2的正方形ABCD沿对角线AC折成直二面角.求:
把边长为2的正方形ABCD沿对角线AC折成直二面角.求: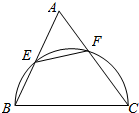
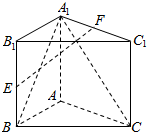 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点,
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点,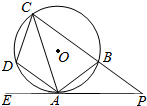 如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.
如图,四边形ABCD内接于⊙O,过点A作⊙O的切钱EP交CB 的延长线于P,己知∠PAB=25°.