题目内容
20、
【解析】解：（Ⅰ）
，
， ……………………2分
由
得
， ……………………3分
所以，
在区间
上单调递减，在区间
上单调递增. ……4分
所以，是函数的极小值点，极大值点不存在. ……5分
（Ⅱ）设切点坐标为
，则
， ………6分
切线的
斜率为
，
所以，
， …………………7分
解得
，
， …
………………8分
所以直线
的方程为
. …………………9分
（Ⅲ）
，
则
， …………………10分
解
，得
，
所以，在区间
上，
为递减函数，
在区间
上，为递增函数. …………………11分
当
，即
时，在区间
上，为递增函数，
所以最小值为
. …………………12分
当
，即
时，的最小值为
.……12分
当
，即
时，在区间上，为递减函数，
所以最小值为
. ………………13分
综上，当时，最小值为
；当时，的最小值
；当时，的
最小值为
.
练习册系列答案
阅读快车系列答案
相关题目
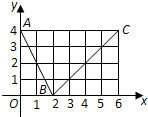如图，函数f（x）的图象是折线段ABC，其中A，B，C的坐标分别为（0，4），（2，0），（6，4），则f（f（0））=