题目内容
如图,点A、B是单位圆 上的两点,点C是圆
上的两点,点C是圆 与
与 轴的正半轴的交点,将锐角
轴的正半轴的交点,将锐角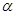 的终边
的终边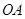 按逆时针方向旋转
按逆时针方向旋转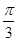 到
到 .
.
(1)若点A的坐标为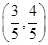 ,求
,求 的值;
的值;
(2)用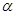 表示
表示 ,并求
,并求 的取值范围.
的取值范围.
(1) ;(2)
;(2) ,
, .
.
解析试题分析:(1)已知单位圆上点 的坐标为
的坐标为 ,根据三角函数的定义有
,根据三角函数的定义有 ,这样我们很快可求得
,这样我们很快可求得 ,也即求出
,也即求出 的值;(2)
的值;(2)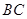 在
在 中,此三角形的两边长为1,
中,此三角形的两边长为1, 而,因此只要应用余弦定理就能求得
而,因此只要应用余弦定理就能求得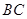 的长,
的长, ,要求其范围,首先求得
,要求其范围,首先求得 的范围,根据已知
的范围,根据已知 ,此时可得
,此时可得 ,那么必有
,那么必有 ,
, 的范围随之而得,
的范围随之而得,  .
.
试题解析:(1)由已知,  (2分)
(2分)
 (4分)
(4分) =
= . (6分)
. (6分)
(2) (8分)
(8分)
 (10分)
(10分) ,
, ,
, (12分)
(12分) (14分)
(14分)
考点:(1)三角函数的定义与求值;(2)余弦定理与三角函数的范围问题.

练习册系列答案
相关题目
 ab.
ab. 中,
中,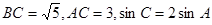
 的值;
的值;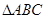 中,角
中,角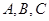 所对的边分别为
所对的边分别为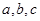 ,点
,点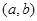 在直线
在直线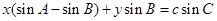 上.
上. 的值;
的值;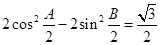 ,且
,且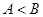 ,求
,求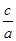 .
.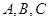 的对边分别为
的对边分别为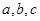 ,且
,且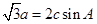 .
.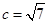 ,且△ABC的面积为
,且△ABC的面积为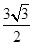 ,求
,求 的值。
的值。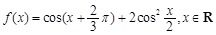 .
. 的值域;
的值域;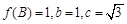 ,求a的值.
,求a的值. ,求C
,求C ,
, ,a=2
,a=2 ,且
,且 ·
· =
=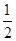 .
. 中,角
中,角 的对边分别为
的对边分别为 且
且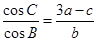 .
.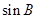 ;
; ,求
,求