题目内容
【题目】已知函数![]() ,其中
,其中![]() .
.
(Ⅰ)讨论函数![]() 的单调性;
的单调性;
(Ⅱ)若![]() ,
,![]() 是方程
是方程![]() 的两个不同的实数根,求证:
的两个不同的实数根,求证:![]() .
.
【答案】(Ⅰ)![]() 在
在![]() 上单调递增.;(Ⅱ)见解析.
上单调递增.;(Ⅱ)见解析.
【解析】
(Ⅰ)对函数求导,![]() 由定义域和已知即可判断
由定义域和已知即可判断![]() 的单调性;
的单调性;
(Ⅱ)根据已知条件列出等式,利用分析法证明即可.
解:(Ⅰ)由题知![]() 的定义域为
的定义域为![]() ,
,
![]() ,
,
由于![]() ,
,![]() ,所以
,所以![]() 恒成立,
恒成立,
故函数![]() 在
在![]() 上单调递增.
上单调递增.
(Ⅱ)因为![]() ,
,![]() 是方程
是方程![]() ,
,
即方程![]() 的两个不同的实数根,
的两个不同的实数根,
所以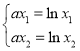 ,所以
,所以![]() ,
,
证法一:设![]() ,
,
则![]() ,
,
可得![]() ,
,![]() ,
,
要证![]() ,
,
只需证![]() ,
,
只需证![]() ,
,
只需证![]() ,
,
只需证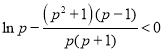 ,
,
考虑到![]() ,
,
只需证![]() .(*)
.(*)
令![]() ,
,
则![]() ,
,
所以![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() ,
,
所以(*)式成立,所以原命题成立.
证法二:由![]() ,
,
得![]() ,
,
所以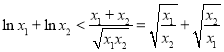 .(*).
.(*).
又要证![]() ,
,
只需证![]() ,
,
只需证![]() ,结合(*)式,
,结合(*)式,
只需证 ,
,
设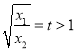 ,只需证明
,只需证明![]() ,
,
构造函数![]() ,只需求证
,只需求证![]() ,
,
由于![]() ,则
,则![]() ,
,
所以![]() 成立,所以得证.
成立,所以得证.

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】![]() 年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的
年初新冠病毒疫情爆发,全国范围开展了“停课不停学”的线上教学活动.哈六中数学组积极研讨网上教学策略:先采取甲、乙两套方案教学,并对分别采取两套方案教学的班级的![]() 次线上测试成绩进行统计如图所示:
次线上测试成绩进行统计如图所示:
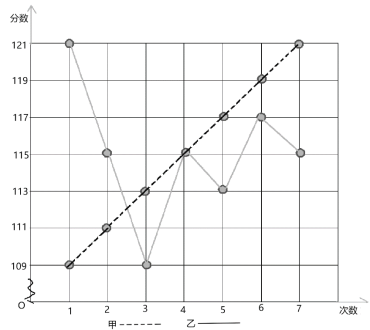
(1)请填写下表(要求写出计算过程)
平均数 | 方差 | |
甲 | ||
乙 |
(2)从下列三个不同的角度对这次方案选择的结果进行
①从平均数和方差相结合看(分析哪种方案的成绩更好);
②从折线图上两种方案的走势看(分析哪种方案更有潜力).