题目内容
如图,有一块半径为1的半圆形钢板,计划剪成矩形ABCD的形状,它的一边AB在圆O的直径上,另一边CD的端点在圆周上.求矩形ABCD面积的最大值和周长的最大值.
【答案】分析:(1)表示出面积,利用基本不等式可得结论;
(2)方法一,利用导数的方法求最值;方法二,利用三角函数的知识求最值.
解答:解:(1)如图,设OB=x,BC=y,∴x2+y2=1,-----------------------------------(1分)
∴ -------------------------------------------(4分)
-------------------------------------------(4分)
当且仅当x=y= 时取等号,即此时,SABCD的最大值是1.-------------------(5分)
时取等号,即此时,SABCD的最大值是1.-------------------(5分)
(2)(方法一) 设矩形ABCD的周长为L,∴L=4x+2y------------------(6分)
设 ,
,
∴y=sinθ,x=cosθ,∴L=4cosθ+2sinθ,L'=-4sinθ+2cosθ,令L'=0,得tan ,-------(8分)
,-------(8分)
而tan ,时,L'>0;而tan
,时,L'>0;而tan ,时,L'<0,∴tan
,时,L'<0,∴tan ,L最大,-----(9分)
,L最大,-----(9分)
此时, ,∴
,∴
 --------------------------------------------(12分)
--------------------------------------------(12分)
(2)(方法二)设矩形ABCD的周长为L,∴L=4x+2y-------------------------(6分)
设 ,∴y=sinθ,x=cosθ,
,∴y=sinθ,x=cosθ,
∴L=4cosθ+2sinθ= =
= --------------(8分)
--------------(8分)
其中, ,
,
∵φ,θ为锐角,
∴φ+θ= 时,
时, ----------------------------------------------(12分)
----------------------------------------------(12分)
点评:本题考查利用数学知识解决实际问题,考查基本不等式、导数知识的运用,属于中档题.
(2)方法一,利用导数的方法求最值;方法二,利用三角函数的知识求最值.
解答:解:(1)如图,设OB=x,BC=y,∴x2+y2=1,-----------------------------------(1分)
∴
 -------------------------------------------(4分)
-------------------------------------------(4分)当且仅当x=y=
 时取等号,即此时,SABCD的最大值是1.-------------------(5分)
时取等号,即此时,SABCD的最大值是1.-------------------(5分)(2)(方法一) 设矩形ABCD的周长为L,∴L=4x+2y------------------(6分)
设
 ,
,∴y=sinθ,x=cosθ,∴L=4cosθ+2sinθ,L'=-4sinθ+2cosθ,令L'=0,得tan
 ,-------(8分)
,-------(8分)而tan
 ,时,L'>0;而tan
,时,L'>0;而tan ,时,L'<0,∴tan
,时,L'<0,∴tan ,L最大,-----(9分)
,L最大,-----(9分)此时,
 ,∴
,∴
 --------------------------------------------(12分)
--------------------------------------------(12分)(2)(方法二)设矩形ABCD的周长为L,∴L=4x+2y-------------------------(6分)
设
 ,∴y=sinθ,x=cosθ,
,∴y=sinθ,x=cosθ,∴L=4cosθ+2sinθ=
 =
= --------------(8分)
--------------(8分)其中,
 ,
,∵φ,θ为锐角,
∴φ+θ=
 时,
时, ----------------------------------------------(12分)
----------------------------------------------(12分)点评:本题考查利用数学知识解决实际问题,考查基本不等式、导数知识的运用,属于中档题.

练习册系列答案
相关题目
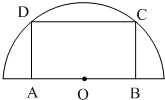 如图,有一块半径为1的半圆形钢板,计划剪成矩形ABCD的形状,它的一边AB在圆O的直径上,另一边CD的端点在圆周上.求矩形ABCD面积的最大值和周长的最大值.
如图,有一块半径为1的半圆形钢板,计划剪成矩形ABCD的形状,它的一边AB在圆O的直径上,另一边CD的端点在圆周上.求矩形ABCD面积的最大值和周长的最大值.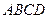 的形状,它的一边
的形状,它的一边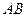 在圆
在圆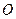 的直径上,另一边
的直径上,另一边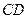 的端点在圆周上.求矩形
的端点在圆周上.求矩形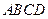 面积的最大值和周长的最大值.
面积的最大值和周长的最大值.
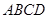 的形状,它的一边
的形状,它的一边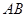 在圆
在圆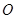 的直径上,另一边
的直径上,另一边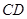 的端点在圆周上.求矩形
的端点在圆周上.求矩形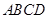 面积的最大值和周长的最大值.
面积的最大值和周长的最大值.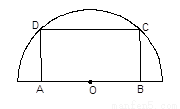
 如图,有一块半径为1的半圆形钢板,计划剪成矩形ABCD的形状,它的一边AB在圆O的直径上,另一边CD的端点在圆周上.求矩形ABCD面积的最大值和周长的最大值.
如图,有一块半径为1的半圆形钢板,计划剪成矩形ABCD的形状,它的一边AB在圆O的直径上,另一边CD的端点在圆周上.求矩形ABCD面积的最大值和周长的最大值.