Question

将一块直角三角板ABO（45^o角）置于直角坐标系中，已知AB=OB=1，AB⊥OB，点P(

1

2

，

1

4

)是三角板内一点，现因三角板中部分受损坏（△POB），要把损坏的部分锯掉，可用经过P的任意一直线MN将其锯成△AMN，问如何确定直线MN的斜率，才能使锯成的△AMN的面积最大？

Answer 1

分析：先由图求得A、B点的坐标，进而表示直线MN的方程，从而求得M、N的坐标，再求得|AN|和点M到直线AN的距离，表示出三角形的面积，再利用其函数的单调性研究．

解答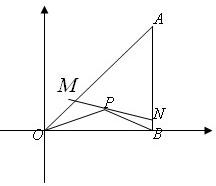：解：由图知A（1，1），B（1，0），kOP=

1

2

，kBP=-

1

2

设直线MN的斜率为k，直线MN与△POB不能相交，所以-

1

2

≤k≤

1

2

直线MN的方程为y-

1

4

=k(x-

1

2

)，
令x=1得y=

2k+1

4

，∴N(1，

2k+1

4

)
令y=x得x=y=

2k-1

4(k-1)

，∴M(

2k-1

4(k-1)

，

2k-1

4(k-1)

)
∴|AN|=1-

2k+1

4

=

3-2k

4

，
点M到直线AN的距离为1-

2k-1

4(k-1)

=

2k-3

4(k-1)

∴S△AMN=

1

2

3-2k

4

•

2k-3

4(k-1)

=

1

8

[(1-k)+

1

4(1-k)

+1]
∵-

1

2

≤k≤

1

2

∴

1

2

≤1-k≤

3

2

而函数y=x+

1

4x

在[

1

2

，+∞)上是增函数，
故当1-k=

3

2

，即k=-

1

2

时∴S_△AMN取得最大值

1

3

．

点评：本题主要考查直线方程及直线的交点，三角形面积及最值的研究方法．