题目内容
经过抛物线
解析:抛物线 的焦点F(1,0),准线方程为x=-1.
的焦点F(1,0),准线方程为x=-1.
由题意设直线l的方程为y=k(x-1) ①
把①代入 得
得

且 ② ∴
② ∴
 即
即
∴弦AB的垂直平分线方程为 , ∴它与准线x=-1的交点C的坐标为
, ∴它与准线x=-1的交点C的坐标为
注意到△ABC为正三角形 ∴ ③
③
又由抛物线定义得 ④
④ 
 ⑤
⑤
∴④⑤代入③解得 ∴所求直线l的斜率的取值范围为
∴所求直线l的斜率的取值范围为 .
.
由题意设直线l的方程为y=k(x-1) ①
把①代入
且
 ② ∴
② ∴∴弦AB的垂直平分线方程为
注意到△ABC为正三角形 ∴
又由抛物线定义得
∴④⑤代入③解得

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
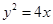 的焦点
的焦点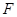 的直线交抛物线于
的直线交抛物线于 两点,满足
两点,满足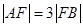 ,则弦
,则弦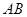 的中点到准线的距离为____.
的中点到准线的距离为____.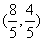 ,线段OP的垂直平分线经过抛物线的焦点F,经过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N 。
,线段OP的垂直平分线经过抛物线的焦点F,经过F作两条互相垂直的弦AB、CD,设AB、CD的中点分别为M、N 。