题目内容
已知经过抛物线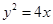
的焦点
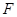的直线交抛物线于
两点，满足
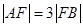，则弦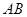
的中点到准线的距离为____．
【答案】
【解析】
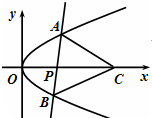
试题分析：设BF=m，由抛物线的定义知AA1=3m，BB1=m，
∴△ABC中，AC=2m，AB=4m，kAB=
，
直线AB方程为y=(x-1)与抛物线方程联立消y得3x2-10x+3=0，
所以AB中点到准线距离为
+1=
+1=。
考点：本题主要考查抛物线的定义及其几何性质。
点评：中档题，利用数形结合思想，分析图形特征，直线与抛物线的关系及焦点弦的问题．常常利用利用抛物线的定义来解决。
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
已知直线l与抛物线y2=8x交于A、B两点，且l经过抛物线的焦点F，A点的坐标为（8，8），则线段AB的中点到准线的距离是（ ）
A、
| ||
B、
| ||
C、
| ||
| D、25 |
设直线l与抛物线y2=2px（p＞0）交于A，B两点，已知当直线l经过抛物线的焦点且与x轴垂直时，△OAB的面积为