题目内容
16．已知x，y＞0，那么$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$的最大值为 （ ）| A． | 2 | B． | $\sqrt{2}$ | C． | 3 | D． | $\sqrt{5}$ |
分析 根据基本不等式的性质即可求出．
解答 解：x，y＞0，（$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$）2=$\frac{x+y+2\sqrt{xy}}{x+y}$=1+$\frac{2\sqrt{xy}}{x+y}$≤1+1=2，当且仅当x=y时取等号，
∴$\frac{\sqrt{x}+\sqrt{y}}{\sqrt{x+y}}$的最大值为 $\sqrt{2}$
故选：B
点评 本题考查了基本不等式的性质，属于中档题．
练习册系列答案
名校课堂系列答案
相关题目
6．
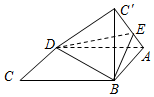如图，将菱形ABCD沿对角线BD折起，使得C点至C′，E点在线段AC′上，若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°，则$\frac{AE}{EC′}$=（ ）
如图，将菱形ABCD沿对角线BD折起，使得C点至C′，E点在线段AC′上，若二面角A-BD-E与二面角E-BD-C′的大小分别为30°和45°，则$\frac{AE}{EC′}$=（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{6}}{6}$ | C． | $\frac{\sqrt{2}}{2}$ | D． | $\frac{\sqrt{6}}{3}$ |