题目内容
已知函数![]() 有如下性质:如果常数
有如下性质:如果常数![]() ,那么该函数在
,那么该函数在![]() 上是减函数,在
上是减函数,在![]() 上是增函数。
上是增函数。
(1)如果函数![]() 在
在![]() 上是减函数,在
上是减函数,在![]() 上是增函数,求
上是增函数,求![]() 的值。
的值。
(2)设常数![]() ,求函数
,求函数![]() 的最大值和最小值;
的最大值和最小值;
(3)当![]() 是正整数时,研究函数
是正整数时,研究函数![]() 的单调性,并说明理由。
的单调性,并说明理由。
解(1) 由已知得![]() =4, ∴
=4, ∴![]() .
.
(2) ∵![]() ∈[1,4], ∴
∈[1,4], ∴![]() ∈[1,2],
∈[1,2],
于是,当x=![]() 时, 函数f(x)=x+
时, 函数f(x)=x+![]() 取得最小值2
取得最小值2![]() .
.
f(1)-f(2)=![]() ,
,
当1≤c≤2时, 函数f(x)的最大值是f(2)=2+![]() ;
;
当2≤c≤4时, 函数f(x)的最大值是f(1)=1+c.
(3)设![]() ,
,![]() .
.
当![]() <x1<x2时, g(x2)>g(x1), 函数g(x)在[
<x1<x2时, g(x2)>g(x1), 函数g(x)在[![]() ,+∞)上是增函数;
,+∞)上是增函数;
当0<x1<x2<![]() 时, g(x2)>g(x1), 函数g(x)在(0,
时, g(x2)>g(x1), 函数g(x)在(0, ![]() ]上是减函数.
]上是减函数.
当n是奇数时,g(x)是奇函数,
函数g(x) 在(-∞,-![]() ]上是增函数, 在[-
]上是增函数, 在[-![]() ,0)上是减函数.
,0)上是减函数.
当n是偶数时, g(x)是偶函数,
函数g(x)在(-∞,-![]() )上是减函数, 在[-
)上是减函数, 在[-![]() ,0]上是增函数.
,0]上是增函数.

练习册系列答案
相关题目
 有如下性质:如果常数
有如下性质:如果常数 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数。
上是增函数。 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值。
的值。 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值; 有如下性质:如果常数
有如下性质:如果常数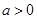 ,那么该函数在
,那么该函数在 上是减函数,在
上是减函数,在 上是增函数;
上是增函数; 在
在 上是减函数,在
上是减函数,在 上是增函数,求
上是增函数,求 的值;
的值;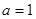 时,试用函数单调性的定义证明函数f(x)在
时,试用函数单调性的定义证明函数f(x)在 上是减函数。
上是减函数。 ,求函数
,求函数 的最大值和最小值;
的最大值和最小值;