题目内容
【题目】在直三棱柱![]() 中,
中, ![]() ,∠ACB=90°,M是
,∠ACB=90°,M是![]() 的中点,N是
的中点,N是![]() 的中点.
的中点.
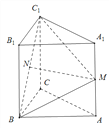
(Ⅰ)求证:MN∥平面![]() ;
;
(Ⅱ)求点![]() 到平面BMC的距离.
到平面BMC的距离.
【答案】(1)见解析;(2)![]() .
.
【解析】试题分析:(1)根据图形取B1C1中点D,连结ND、A1D,得到四边形A1MND为平行四边形,从而得到线面平行。(2)先证得BC⊥平面A1MC1,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离,从而得到点面距离。
解析:
(1)如图所示,取B1C1中点D,连结ND、A1D ∴DN∥BB1∥AA1
又DN=![]() ,∴四边形A1MND为平行四边形。
,∴四边形A1MND为平行四边形。
∴MN∥A1 D 又MN ![]() 平面A1B1C1,AD1
平面A1B1C1,AD1![]() 平面A1B1C1 ∴MN∥平面
平面A1B1C1 ∴MN∥平面![]()
(2)因三棱柱![]() 为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
为直三棱柱, ∴C1 C ⊥BC,又∠ACB=90°∴BC⊥平面A1MC1
在平面ACC1 A1中,过C1作C1H⊥CM,又BC⊥C1H,故C1H为C1点到平面BMC的距离。
在等腰三角形CMC1中,C1 C=2![]() ,CM=C1M=
,CM=C1M=![]() ∴.
∴. ![]() 。
。

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目