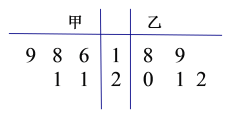
题目内容
【题目】已知函数f(x)=x﹣2sinx.
(Ⅰ)求函数f(x)在 ![]() 上的最值;
上的最值;
(Ⅱ)若存在 ![]() ,使得不等式f(x)<ax成立,求实数a的取值范围.
,使得不等式f(x)<ax成立,求实数a的取值范围.
【答案】解:(Ⅰ)f'(x)=1﹣2cosx, ![]()
x |
|
|
|
|
|
|
|
y' | + | 0 | ﹣ | 0 | + | ||
y |
| ↗ | 极大值 | ↘ | 极小值 | ↗ |
|
![]()
(Ⅱ)f(x)<ax,
∴2sinx﹣(1﹣a)x>0
设g(x)=2sinx﹣(1﹣a)x,则g'(x)=2cosx﹣(1﹣a)
由 ![]()
①1﹣a≥2即a≤﹣1,此时g'(x)<0得出g(x)在 ![]() 单调递减,g(x)<g(0)=0不成立
单调递减,g(x)<g(0)=0不成立
②1﹣a≤0即a≥1,此时g'(x)>0得出g(x)在 ![]() 单调递增,g(x)>g(0)=0成立
单调递增,g(x)>g(0)=0成立
③0<1﹣a<2即﹣1<a<1,令 ![]() ,存在唯一
,存在唯一 ![]() ,使得
,使得 ![]() .当x∈(0,x0)时,g'(x)>0得出g(x)>g(0)=0,
.当x∈(0,x0)时,g'(x)>0得出g(x)>g(0)=0,
∴存在 ![]() ,有g(x)>0成立
,有g(x)>0成立
综上可知:a>﹣1
【解析】(1)求出导函数,得出极值点,根据极值点求闭区间函数的最值;(2)不等式整理得出2sinx﹣(1﹣a)x>0,构造函数,根据导函数进行分类讨论,即最大值大于零即可.

【题目】微信是现代生活进行信息交流的重要工具,据统计,某公司![]() 名员工中
名员工中![]() 的人使用微信,其中每天使用微信时间在一小时以内的有
的人使用微信,其中每天使用微信时间在一小时以内的有![]() 人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于
人,其余每天使用微信在一小时以上.若将员工年龄分成青年(年龄小于![]() 岁)和中年(年龄不小于
岁)和中年(年龄不小于![]() 岁)两个阶段,使用微信的人中
岁)两个阶段,使用微信的人中![]() 是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中
是青年人.若规定:每天使用微信时间在一小时以上为经常使用微信,经常使用微信的员工中![]() 是青年人.
是青年人.
(Ⅰ)若要调查该公司使用微信的员工经常使用微信与年龄的关系,列出![]() 列联表;
列联表;
青年人 | 中年人 | 合计 | |
经常使用微信 | |||
不经常使用微信 | |||
合计 |
(Ⅱ)由列联表中所得数据,是否有![]() 的把握认为“经常使用微信与年龄有关”?
的把握认为“经常使用微信与年龄有关”?
(Ⅲ)采用分层抽样的方法从“经常使用微信”的人中抽取![]() 人,从这
人,从这![]() 人中任选
人中任选![]() 人,求事件
人,求事件![]() “选出的
“选出的![]() 人均是青年人”的概率.
人均是青年人”的概率.
附:
|
|
|
|
|
|
【题目】国家射击队的某队员射击一次,命中7~10环的概率如表所示:
命中环数 | 10环 | 9环 | 8环 | 7环 |
概率 | 0.32 | 0.28 | 0.18 | 0.12 |
求该射击队员射击一次 求:
(1)射中9环或10环的概率;
(2)至少命中8环的概率;(3)命中不足8环的概率。