题目内容
已知向量 =
=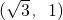 ,
, =(0,-1),
=(0,-1), =
= .若
.若 -2
-2 与
与 共线,则k=
共线,则k=
- A.1
- B.

- C.-1
- D.3
A
分析:先求出 的坐标,再根据两个向量共线的性质可得
的坐标,再根据两个向量共线的性质可得  ,由此解得 k 的值.
,由此解得 k 的值.
解答:∵向量 =
=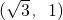 ,
, =(0,-1),
=(0,-1), =
= ,
,
∴ =(
=( ,3).
,3).
∵向量 -2
-2 与
与 共线,
共线,
∴ ,解得 k=1,
,解得 k=1,
故选A.
点评:本题主要考查两个向量的加减法的法则,两个向量共线的性质,两个向量坐标形式的运算,属于基础题.
分析:先求出
 的坐标,再根据两个向量共线的性质可得
的坐标,再根据两个向量共线的性质可得  ,由此解得 k 的值.
,由此解得 k 的值.解答:∵向量
 =
=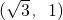 ,
, =(0,-1),
=(0,-1), =
= ,
,∴
 =(
=( ,3).
,3).∵向量
 -2
-2 与
与 共线,
共线,∴
 ,解得 k=1,
,解得 k=1,故选A.
点评:本题主要考查两个向量的加减法的法则,两个向量共线的性质,两个向量坐标形式的运算,属于基础题.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知向量
=(1,0),
=(1,1),则|
|等于( )
| OA |
| OB |
| AB |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|