题目内容
定义在（0，+∞）上的可导函数f（x）满足：x•f′（x）＜f（x）且f（1）=0，则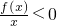
的解集为
- A.（0，1）
- B.（0，1）∪（1，+∞）
- C.（1，+∞）
- D.?
C
分析：先确定f'（x）＜0得到函数f（x）是单调递减的，然后令
＜0即可得到答案．
解答：函数f（x）的定义域为x＞0，所以f（x）＜0，
f（x）＜0时，
xf'（x）＜f（x），
则xf'（x）＜0，
∵x＞0
∴f'（x）＜0
∴函数f（x）在（0，+∞）上为减函数，
∵f（1）=0
f（x）＜0=f（1）
解得x＞1，
故选C．
点评：本题主要考查函数的单调性与其导函数之间的关系，考查了学生的计算能力，属基础题．
分析：先确定f'（x）＜0得到函数f（x）是单调递减的，然后令
＜0即可得到答案．解答：函数f（x）的定义域为x＞0，所以f（x）＜0，
f（x）＜0时，
xf'（x）＜f（x），
则xf'（x）＜0，
∵x＞0
∴f'（x）＜0
∴函数f（x）在（0，+∞）上为减函数，
∵f（1）=0
f（x）＜0=f（1）
解得x＞1，
故选C．
点评：本题主要考查函数的单调性与其导函数之间的关系，考查了学生的计算能力，属基础题．
练习册系列答案
相关题目
已知定义在（0，1）上的函数f（x），对任意的m，n∈（1，+∞）且m＜n时，都有f(
)-f(
)=f(
)记an=f(
)，n∈N*，则在数列{an}中，a1+a2+…a8=（ ）
| 1 |
| n |
| 1 |
| m |
| m-n |
| 1-mn |
| 1 |
| n2+5n+5 |
A、f(
| ||
B、f(
| ||
C、f(
| ||
D、f(
|