题目内容
（2013•广东模拟）已知向量
=(sinx，
)，
=(cosx，-1)．
（1）当
∥
时，求cos2x-sin2x的值；
（2）设函数f(x)=2(
+
)•
，已知在△ABC中，内角A、B、C的对边分别为a、b、c，若a=
，b=2，sinB=
，若f(x0)+cos(2A+
)=-
+
，x0∈[
，
]，求cos2x0的取值范围．
| a |
| 3 |
| 4 |
| b |
（1）当
| a |
| b |
（2）设函数f(x)=2(
| a |
| b |
| b |
| 3 |
| ||
| 3 |
| π |
| 6 |
| 1 |
| 2 |
3
| ||
| 5 |
| π |
| 8 |
| π |
| 2 |
分析：（1）由
∥
，结合向量平行的坐标表示可求tanx，然后利用二倍角公式及同角基本关系对cos2x-sin2x进行化简，代入即可求解
（2）利用向量的数量积的坐标表示及和差角、辅助角公式对已知函数化简可得f(x)=2(
+
)•
=
sin(2x+
)+
，然后结合正弦定理可求A，代入f(x)+cos(2A+
)，化简可求
| a |
| b |
（2）利用向量的数量积的坐标表示及和差角、辅助角公式对已知函数化简可得f(x)=2(
| a |
| b |
| b |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
，然后结合正弦定理可求A，代入f(x)+cos(2A+
| π |
| 6 |
解答：解：（1）∵
∥
，
∴
cosx+sinx=0，
∴tanx=-
…（2分）
cos2x-sin2x=
=
=
…（6分）
（2）f(x)=2(
+
)•
=
sin(2x+
)+
由正弦定理得
=
可得sinA=
，所以A=
，…（9分）
f(x)+cos(2A+
)=
sin(2x+
)-
，
∵f(x0)+cos(2A+
)=-
+
，x0∈[
，
]，
∴sin(2x0+
)=
，cos(2x0+
)=-
| a |
| b |
∴
| 3 |
| 4 |
∴tanx=-
| 3 |
| 4 |
cos2x-sin2x=
| cos2x-2sinxcosx |
| sinx2+cos2x |
| 1-2tanx |
| 1+tan2x |
| 8 |
| 5 |
（2）f(x)=2(
| a |
| b |
| b |
| 2 |
| π |
| 4 |
| 3 |
| 2 |
由正弦定理得
| a |
| sinA |
| b |
| sinB |
| ||
| 2 |
| π |
| 4 |
f(x)+cos(2A+
| π |
| 6 |
| 2 |
| π |
| 4 |
| 1 |
| 2 |
∵f(x0)+cos(2A+
| π |
| 6 |
| 1 |
| 2 |
3
| ||
| 5 |
| π |
| 8 |
| π |
| 2 |
∴sin(2x0+
| π |
| 4 |
| 3 |
| 5 |
| π |
| 4 |
| 4 |
| 5 |
点评：本题主要考查了向量平行的坐标表示及二倍角公式、同角基本关系、和差角公式等知识的综合应用．
练习册系列答案
阅读快车系列答案
相关题目
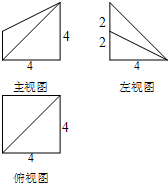（2013•广东模拟）一几何体的三视图如图所示，则这个几何体的体积为