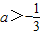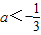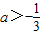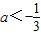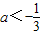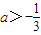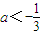题目内容
若函数y=e(a-1)x+4x(x∈R)有大于零的极值点,则实数a范围是
- A.a>-3
- B.a<-3
- C.
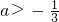
- D.
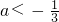
B
分析:由题意可得:y′=(a-1)e(a-1)x+4(a<1),即可得到函数的零点为x0=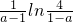 ,所以x0=
,所以x0=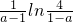 >0,进而求出a的范围.
>0,进而求出a的范围.
解答:因为函数y=e(a-1)x+4x,
所以y′=(a-1)e(a-1)x+4(a<1),
所以函数的零点为x0=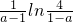 ,
,
因为函数y=e(a-1)x+4x(x∈R)有大于零的极值点,
所以x0=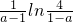 >0,即
>0,即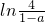 <0,
<0,
解得:a<-3.
故选B.
点评:本题主要考查利用导数求函数的极值点,以及对数函数的单调性等知识点,此题属于基础题.
分析:由题意可得:y′=(a-1)e(a-1)x+4(a<1),即可得到函数的零点为x0=
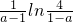 ,所以x0=
,所以x0=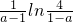 >0,进而求出a的范围.
>0,进而求出a的范围.解答:因为函数y=e(a-1)x+4x,
所以y′=(a-1)e(a-1)x+4(a<1),
所以函数的零点为x0=
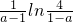 ,
,因为函数y=e(a-1)x+4x(x∈R)有大于零的极值点,
所以x0=
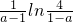 >0,即
>0,即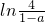 <0,
<0,解得:a<-3.
故选B.
点评:本题主要考查利用导数求函数的极值点,以及对数函数的单调性等知识点,此题属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目