题目内容
空间四边形ABCD的两条对角线AC=4，BD=6，则平行于两对角线的截面四边形EFGH的周长的取值范围是分析：先由“平行于两对角线的截面四边形EFGH”得到四边形为平行四边形，从而有各点分所在边成相同的比例，再由三角形相似结合两对角线，表示出来四边形EFGH的相邻两边：EF=
=
，EH=
=
，从而构建周长函数模型，最后得到结论．
| AC•BE |
| AB |
| 4BE |
| AB |
| AE•BD |
| AB |
| 6AE |
| AB |
解答：解：设E、F、G、H分别在AB、BC、CD、DA上，
∵截面四边形EFGH平行于两对角线
∴EFGH是平行四边形．
∴由三角形相似：
=
∴EF=
=
又∵
=
∴EH=
=
∴截面平行四边形EFGH的周长C=2（EF+EH）=2（
+
）=8+
∵0＜AE＜AB，
∴周长的取值范围为：8＜C＜12
故答案为：（8，12）
∵截面四边形EFGH平行于两对角线
∴EFGH是平行四边形．
∴由三角形相似：
| EF |
| AC |
| BE |
| AB |
∴EF=
| AC•BE |
| AB |
| 4BE |
| AB |
又∵
| EH |
| BD |
| AE |
| AB |
∴EH=
| AE•BD |
| AB |
| 6AE |
| AB |
∴截面平行四边形EFGH的周长C=2（EF+EH）=2（
| 4BE |
| AB |
| 6AE |
| AB |
| 4AE |
| AB |
∵0＜AE＜AB，
∴周长的取值范围为：8＜C＜12
故答案为：（8，12）
点评：本题主要考查棱锥的结构特征，特别考查了截面问题，三角形相似以及建模和解模的能力，属中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
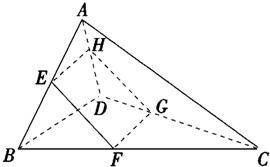空间四边形ABCD的两条对棱AC、BD的长分别为5和4，则平行于两条对棱的截面四边形EFGH在平移过程中，周长的取值范围是
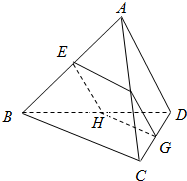空间四边形ABCD的对棱AD，BC成60°的角，且AD=BC=a，平行于AD与BC的截面分别交AB，AC，CD，BD于E、F、G、H．
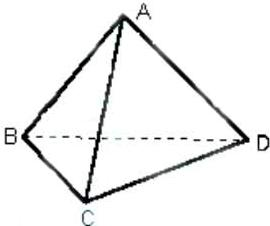如图，一空间四边形ABCD的对边AB与CD，AD与BC都互相垂直，用向量证明：AC与BD也互相垂直．