题目内容

在直角坐标系中，已知椭圆的中心为坐标原点，右焦点为（为常数，且），过作倾斜角为的直线交椭圆于，两点，为线段的中点，射线交椭圆于点，四边形是平行四边形．

（1）求椭圆的方程；

（2）判断椭圆与线段是否有公共点？

（1） 

（2）或时，椭圆与线段没有公共点；时，椭圆与线段有公共点


解析:

（1）依题意，设椭圆的方程为，

直线的方程为．

将代入中，整理得．①

记，，，则，是方程①的两个不同的根，

又四边形是平行四边形，则．

点在椭圆上，

即解得

故所求椭圆的方程为．

（2）将代入中，整理得．

令．

则椭圆与线段有公共点时，的取值范围等价于函数的值域．

的值域为，当，即时，椭圆与线段有公共点．

当或，即或时，椭圆与线段没有公共点．

练习册系列答案
相关题目
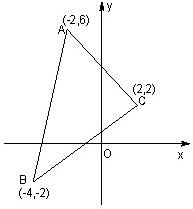精英家教网如图，在直角坐标系中，已知△ABC的三个顶点的坐标，求：
（1）直线AB的一般式方程；
（2）AC边上的高所在直线的斜截式方程．
在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：x+
3
y=0（x≥0），过点P（1，0）作直线分别交射线OA，OB于A，B点．
（1）当AB中点为P时，求直线AB的方程；
（2）在（1）的条件下，若A、B两点到直线l：y=mx+2的距离相等，求实数m的值．
在直角坐标系中，已知A（cosx，sinx），B=（1，1），O为坐标原点，
OA
+
OB
=
OC
，f（x）=|
OC
|2．
（Ⅰ）求f（x）的对称中心的坐标及其在区间[-π，0]上的单调递减区间；
（Ⅱ）若f（x0）=3+
2
，x0∈[
π
2
，
3π
4
]，求tanx0的值．
（2007•普陀区一模）在直角坐标系中，已知点列P1（1，-
1
2
），P2（2，
1
22
），P3（3，-
1
23
），…，Pn（n，(-
1
2
)n），…，其中n是正整数．连接P1 P2的直线与x轴交于点X1（x1，0），连接P2 P3的直线与x轴交于点X2（x2，0），…，连接Pn Pn+1的直线与x轴交于点Xn（xn，0），…．
（1）求数列{an}的通项公式；
（2）依次记△X1P2X2的面积为S1，△X2P3X3的面积为S3，…，△XnPn+1Xn的面积为Sn，…试求无穷数列{Sn}的各项和．
精英家教网如图，在直角坐标系中，已知射线OA：x-y=0（x≥0），OB：
3
x+3y=0（x≥0），过点P（a，0）（a＞0）作直线l分别交射线OA，OB于A，B两点，且
AP
=2
PB
，则直线l的斜率为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网