题目内容
已知函数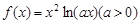
(Ⅰ)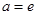 时,求
时,求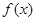 在
在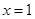 处的切线方程;
处的切线方程;
(Ⅱ)若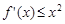 对任意的
对任意的 恒成立,求实数
恒成立,求实数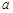 的取值范围;
的取值范围;
(Ⅲ)当 时,设函数
时,设函数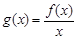 ,若
,若 ,求证:
,求证: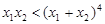 .
.
【答案】
(Ⅰ) ;(Ⅱ)
;(Ⅱ) ;(Ⅲ)详见解析.
;(Ⅲ)详见解析.
【解析】
试题分析:(Ⅰ)将 代入,求导即得;(Ⅱ)
代入,求导即得;(Ⅱ) ,即
,即 在
在 上恒成立. 不等式恒成立的问题,一般有以下两种考虑,一是分离参数,二是直接求最值.在本题中,设
上恒成立. 不等式恒成立的问题,一般有以下两种考虑,一是分离参数,二是直接求最值.在本题中,设 ,则
,则 ,这里面不含参数
,这里面不含参数 了,求
了,求 的最大值比较容易了,所可直接求最大值.(Ⅲ)本题首先要考虑的是,所要证的不等式与函数
的最大值比较容易了,所可直接求最大值.(Ⅲ)本题首先要考虑的是,所要证的不等式与函数 有什么关系?待证不等式可作如下变形:
有什么关系?待证不等式可作如下变形:
 ,最后这个不等式与
,最后这个不等式与 有联系吗?我们再往下看.
有联系吗?我们再往下看.
 ,所以在
,所以在 上
上 是增函数.
是增函数.
因为 ,所以
,所以
即 从这儿可以看出,有点联系了.
从这儿可以看出,有点联系了.
同理 ,
,
所以 ,
,
与待证不等式比较,只要 问题就解决了,而这由重要不等式可证,从而问题得证.
问题就解决了,而这由重要不等式可证,从而问题得证.
试题解析:(Ⅰ) ,
, ,所以切线为:
,所以切线为: 即
即 .
3分
.
3分
(Ⅱ) ,
, ,即
,即 在
在 上恒成立
上恒成立
设 ,
, ,
, 时,单调减,
时,单调减, 单调增,
单调增,
所以 时,
时, 有最大值.
有最大值. ,
,
所以 .
8分
.
8分
法二、 可化为
可化为 .
.
令 ,则
,则 ,所以
,所以
所以 .
.
(Ⅲ)当 时,
时, ,
,  ,所以在
,所以在 上
上 是增函数,
是增函数, 上是减函数.
上是减函数.
因为 ,所以
,所以
即 ,同理
,同理 .
.
所以
又因为 当且仅当“
当且仅当“ ”时,取等号.
”时,取等号.
又 ,
, ,
,
所以 ,所以
,所以 ,
,
所以: .
14分
.
14分
考点:1、导数的应用;2、不等式的证明.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目

 .
. 的解集;
的解集; 对
对 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
 满足
满足 ,且
,且 时,
时, ,则
,则 的图象的交点个数为
的图象的交点个数为

 时,函数
时,函数 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围; 的最小值;
的最小值; 的图象C1与函数
的图象C1与函数 的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线互相平行?若存在,求出R的横坐标;若不存在,请说明理由。
的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线互相平行?若存在,求出R的横坐标;若不存在,请说明理由。 .
.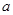 =1时,求
=1时,求 的值域;
的值域; 的解集是全体实数,求
的解集是全体实数,求