题目内容
(本小题共12分)
已知函数
(Ⅰ)若 时,函数
时,函数 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(Ⅱ)在(1)的结论下,设函数 的最小值;
的最小值;
(Ⅲ)设函数 的图象C1与函数
的图象C1与函数 的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线互相平行?若存在,求出R的横坐标;若不存在,请说明理由。
的图象C2交于P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线互相平行?若存在,求出R的横坐标;若不存在,请说明理由。
【答案】
(Ⅰ)依题意:
∵ 上是增函数,∴
上是增函数,∴ 恒成立,…(2分)
恒成立,…(2分)
∴ ∵
∵ ∴b的取值范围为
∴b的取值范围为 …………(4分)
…………(4分)
(Ⅱ)设
∵ ∴当
∴当 上为增函数,
上为增函数,
当t=1时, ………………………………………… (5分)
………………………………………… (5分)
当
 ……………… (6分)
……………… (6分)
当 上为减函数,
上为减函数,
当t=2时, …………………………………………………………(7分)
…………………………………………………………(7分)
综上所述,当
当
 …………………………………………… (8分)
…………………………………………… (8分)
(Ⅲ)设点P、Q的坐标是
则点M、N的横坐标为
C1在M处的切线斜率为 C2在点N处的切线斜率
C2在点N处的切线斜率
假设C1在点M处的切线与C2在点N处的切线平行,则
即
则




 ……………………(10分)
……………………(10分)
设 …………………………①
…………………………①
令 则
则
∵ ∴
∴ 所以
所以 上单调递增,故
上单调递增,故
则 这与①矛盾,假设不成立
这与①矛盾,假设不成立
故C1在点M处的切线与C2在点N处的切线不平行。……………… (12分)
【解析】略

练习册系列答案
 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
 ⊥平面
⊥平面 ,
, ∥
∥ 是正三角形,
是正三角形, ,且
,且 是
是 的中点
的中点
 ∥平面
∥平面 ;
; .
. 名,女同学有
名,女同学有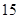 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个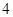 人的课外兴趣小组.
人的课外兴趣小组. 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;


 ,
, ,求证:
,求证: .
. 的值.
的值.